SOLUTION: PLEASE HELP ME TO SOLVE THESE QUESTIONS............. Q1.IF {{{x^3+1/x^3=2}}} then find the value of x+1/x Q2.FIND THE VALUE OF {{{(x+y)^3+(x-2y+2)}}} Q3.IF {{{(x+1/x)*(x-1

Algebra ->  Numeric Fractions Calculators, Lesson and Practice -> SOLUTION: PLEASE HELP ME TO SOLVE THESE QUESTIONS............. Q1.IF {{{x^3+1/x^3=2}}} then find the value of x+1/x Q2.FIND THE VALUE OF {{{(x+y)^3+(x-2y+2)}}} Q3.IF {{{(x+1/x)*(x-1      Log On


   

Question 353546: PLEASE HELP ME TO SOLVE THESE QUESTIONS.............
Q1.IF x%5E3%2B1%2Fx%5E3=2 then find the value of x+1/x
Q2.FIND THE VALUE OF 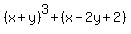%28x%2By%29%5E3%2B%28x-2y%2B2%29
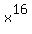
Q3.IF .then find the value of x%5E16



Found 2 solutions by Edwin McCravy, jsmallt9:
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
PLEASE HELP ME TO SOLVE THESE QUESTIONS.............
Q1.IF x%5E3%2B1%2Fx%5E3=2 then find the value of x+1/x
Using the binomial theorem:

%28x%2B1%2Fx%29%5E3=x%5E3%2B3x%5E2%281%2Fx%29%2B3x%281%2Fx%29%5E2%2B%281%2Fx%29%5E3%29

%28x%2B1%2Fx%29%5E3=x%5E3%2B3x%2B3x%281%2Fx%5E2%29%2B1%2Fx%5E3

%28x%2B1%2Fx%29%5E3=x%5E3%2B3x%2B3%2Fx%2B1%2Fx%5E3

%28x%2B1%2Fx%29%5E3=x%5E3%2B1%2Fx%5E3%2B3x%2B3%2Fx

%28x%2B1%2Fx%29%5E3=%28x%5E3%2B1%2Fx%5E3%29%2B3%28x%2B1%2Fx%29

and since we are given x%5E3%2B1%2Fx%5E3=2,

%28x%2B1%2Fx%29%5E3=2%2B3%28x%2B1%2Fx%29

%28x%2B1%2Fx%29%5E3-3%28x%2B1%2Fx%29-2=0

Let y+=+x%2B1%2Fx, which is what we want to find.

y%5E3-3y-2=0

Feasible rational roots are ±1, ±2
Using synthetic division we find that -1 is a solution

-1|1  0 -3 -2
  |  -1  1  2
   1 -1 -2  0

Thus we have factored

y%5E3-3y-2=0

as

%28y%2B1%29%28y%5E2-y-2%29=0

Factoring further:

%28y%2B1%29%28y%2B1%29%28y-2%29=0

Thus the solutions are y = -1, y = 2

so x%2B1%2Fx is either -1 or 2.

-----------------------------------

Q2.FIND THE VALUE OF %28x%2By%29%5E3%2B%28x-2y%2B2%29
%28x%2By%29%5E3%2B%28x-2y%2B2%29
Something is missing from this one that must be given 
to find a solution.  Check the problem again and repost 
it with the part that's missing here.

-----------------------------------

Q3.IF .then find the value of x%5E16


Multiplying the first two factors:



Multiplying the first two factors:

%28x%5E4-1%2Fx%5E4%29%2A%28x%5E4%2B1%2Fx%5E4%29%2A%28x%5E8%2B1%2Fx%5E8%29=3%2F2

Multiplying the first two factors:

%28x%5E8-1%2Fx%5E8%29%2A%28x%5E8%2B1%2Fx%5E8%29=3%2F2

Multiplying those factors:

x%5E16-1%2Fx%5E16=3%2F2

Let y+=+x%5E16

y-1%2Fy=3%2F2

Clear of fractions:

2y%5E2-2=3y

2y%5E2-3y-2=0

Factoring,

%28y-2%29%282y%2B1%29=0

Solutions are y+=+2, y=-1%2F2

and since y=x%5E16

x%5E16=2 or x%5E16=-1%2F2

(In the case of the second negative solution, 
x would have to be imaginary).

Edwin

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Q1.IF x%5E3%2B1%2Fx%5E3=2 then find the value of x+1/x
Let's start by eliminating the fraction. Multiply both sides by x%5E3:
x%5E6+%2B+1+=+2x%5E3
To solve a non-linear equation, we often get one side equal to zero and factor:
x%5E6+-+2x%5E3+%2B+1+=+0
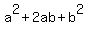Solving this equation is much easier if we notice that the exponent of 6 is twice the exponent of 3. That makes this equation in quadratic form for x%5E3. Looking at the expression this way we can, perhaps, see that the expression fits the pattern: a%5E2+%2B+2ab+%2B+b%5E2 which we know is, in factored form: %28a%2Bb%29%5E2. So you equation factors into:
x%5E3+-+1%29%5E2+=+0
By the Zero Product Property we know that this (or any) product is zero only if one of the factors is zero. So:
x%5E3+-+1+=+0
Solving this we get x = 1.
This makes x + 1/x = 1 + 1/1 = 1 + 1 = 2.

Q2.FIND THE VALUE OF 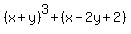%28x%2By%29%5E3%2B%28x-2y%2B2%29
This problem does not make sense. You can't find a value unless you have an equation and this has no equals sign. The only thing you can do with this expression is simplify it. That means cubing (x+y) correctly (Hint: It is not x%5E3+%2B+y%5E3!) and then combining like terms, if any.

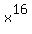
Q3.IF .then find the value of x%5E16
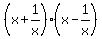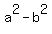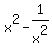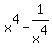The first two factors%28x%2B1%2Fx%29%2A%28x-1%2Fx%29 fit the pattern of (a+b)(a-b) which we know from the pattern to be equal to a%5E2+-+b%5E2. So your first two factors are equal to x%5E2+-+1%2Fx%5E2. But this and the third factor fit the same pattern again. So the first three factors are equal to x%5E4+-+1%2Fx%5E4. But this, combined with the next factor fit the pattern again. And this repeats once more time making the entire left side of the equation equal to:
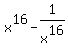x%5E16+-+1%2Fx%5E16. So now our equation looks like:
x%5E16+-+1%2Fx%5E16+=+3%2F2
We can solve this just like we did problem 1. Get rid of the fraction:
x%5E32+-+1+=+%283%2F2%29x%5E16
Get one side equal to zero:
x%5E32+-+%283%2F2%29x%5E16+-+1+=+0
This, like problem 1, is an equation in "quadratic form". This time it is in quadratic form for 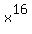x%5E16. This equation, unlike problem 1, does not factor easily. When we can't factor, we resort to the Quadratic Formula. This gives us:
x%5E16+=+%28-%28-3%2F2%29+%2B-+sqrt%28%28-3%2F2%29%5E2+-+4%281%29%28-1%29%29%29%2F2%281%29
Simplifying.
x%5E16+=+%28-%28-3%2F2%29+%2B-+sqrt%289%2F4+-+4%281%29%28-1%29%29%29%2F2%281%29
x%5E16+=+%283%2F2+%2B-+sqrt%289%2F4+%2B+4%29%29%2F2
x%5E16+=+%283%2F2+%2B-+sqrt%289%2F4+%2B+16%2F4%29%29%2F2
x%5E16+=+%283%2F2+%2B-+sqrt%2825%2F4%29%29%2F2
x%5E16+=+%283%2F2+%2B-+5%2F2%29%2F2
In long form this is:
x%5E16+=+%283%2F2+%2B+5%2F2%29%2F2 or x%5E16+=+%283%2F2+-+5%2F2%29%2F2
Looking at the second equation, we see that the fraction will be negative. And since 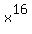x%5E16 cannot be equal to a negative number, there will be no solutions to the second equation. So we only have to solve the first equation. we continue by simplifying:
x%5E16+=+%288%2F2%29%2F2
x%5E16+=+4%2F2
x%5E16+=+2