SOLUTION: Find numerical values for all simultaneous solutions of: X^2+3y^2=27 xy=6 and illustrate with a graph

Algebra ->  Linear-equations -> SOLUTION: Find numerical values for all simultaneous solutions of: X^2+3y^2=27 xy=6 and illustrate with a graph      Log On


   

Question 353523: Find numerical values for all simultaneous solutions of:
X^2+3y^2=27
xy=6
and illustrate with a graph
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2+%2B+3%2Ax%5E2=27 (1)
xy+=+6 (2)
From equation (2), y+=+6%2Fx.
Substituting into (1),
x%5E2+%2B3%2A%286%2Fx%29%5E2=27,
x%5E2+%2B+108%2Fx%5E2=27,
Multiplying both sides by x%5E2, we get
x%5E4+%2B108+=+27%2Ax%5E2, or
x%5E4+-+27%2Ax%5E2+%2B+108+=+0. Treating the equation as a quadratic equation in x%5E2, and applying the quadratic formula, we get
x%5E2+=+%2827+%2B-+sqrt%2827%5E2-4%2A1%2A108%29%29%2F2,
x%5E2+=+%2827%2B-sqrt%28297%29%29%2F2. Hence
x+=+sqrt%28%2827%2B-sqrt%28297%29%29%2F2%29, or
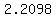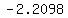x+=+-sqrt%28%2827%2B-sqrt%28297%29%29%2F2%29. The values that we get from the first x-value are x+=+4.703 or 2.2098. from the second x-value, we get the negatives:x+=+-4.703 or -2.2098.
The corresponding y-values are (obtained from equation (2)) 1.2758, 2.7152,
-1.2758, -2.7152.