Question 352757: What are three consecutive numbers that have a sum which is 1/5 of their product?
Answer by jrfrunner(365)   (Show Source):
You can put this solution on YOUR website! 3 consecutive numbers: x, x+1, x+2
--
sum is 1/5 their product: x+(x+1)+(x+2)=1/5[x*(x+1)*(x+2)]
--
x+(x+1)+(x+2)=1/5[x*(x+1)*(x+2)]
--
since highest power is cubed, there are a total of 3 roots
--
by descartes sign test, there is one positive real root
possible real roots -+1,-+3,-+5,-+15
actual roots will rarely be in the extremes, so try near the middle, try 3
via synthetic division.
--
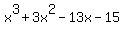 divided by root 3 yields 
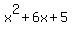
in other words
--
factor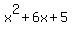
(x+5)*(x+1)
--
Therefore: 
with potentially 3 solutions
if x=3, then x+1=4 and x+2=5
if x=-5 then x+1=-4 and x+2=-3
if x=-1 then x+1=0 and x+2=1
--
(3,4,5) or (-5,-4,-3) or (-1,0,1)
==
validate each set of solutions
--
(3,4,5)
sum=3+4+5=12
1/5 product= 1/5*(3*4*5)=60/5=12
--
(-5,-4,-3)
sum=-5-4-3=-12
1/5 product= 1/5*(-5)*(-4)*(-3)=-60/5=-12
--
(1,0,-1)
sum=1+0-1=0
1/5 product = 1/5*(1)*(0)*(-1)=0/5=0
--
so there exists more than one solution. All three of these solutions work.
|
|
|
