|
Question 352453: Use rational exponents to write an exponent of 4 SQRT(x) * an exponent of 3 SQRT(6x) as a single radical expression??
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I assume the expression is:
If this is correct, the first radical is read: "the fourth root of x" and the second radical is read: "the third root of 6x" or "the cube root of 6x". The 4 and the 3 are not exponents (although, as you'll see shortly, they do become denominators of fractional exponents).
Another word for "rational" (in Math) is "fractional". So the problem is saying: "Use fractional exponents to ..." This means we need to know how to change radicals into fractional exponents (and vice versa). The connection between radicals and exponents is:
(Note: square roots are "second roots". IOW,  is the same thing as  .)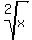
So your expression, written with fractional exponents instead of radicals is:
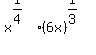
(Note: Are you sure the 6 is in the problem? It makes the problem much harder.) Using the the rule for exponents,  , on the 6x part of the above expression we get:
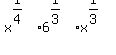
To multiply the "x" parts of the above we will use a rule for exponents,  , which says we should add the exponents:
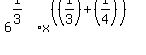
To add the exponents, which are fractions, we must, of course, have common denominators:
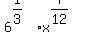
To combine the 6 part and the "x" part of the above we will use the rule again (in the opposite direction this time). Once again we need a common denominator:
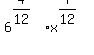
Factoring out a 1/12 in each exponent we get:
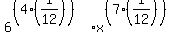
Now we can use the rule (from right to left this time):
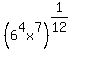
Now, since 1/12 as an exponent means 12th root, we can rewrite the above as the radical:
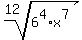
The only thing left is to multiply out  . I'll leave that to you and your calculator. (It should work out to be a number somewhere near 1300.)
|
|
|
| |
