Find the exact value of 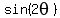 if
if  and
and 
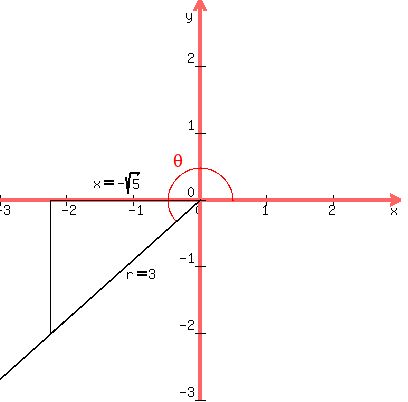
We draw the approximate graph of the angle  in quadrant III,
since it is between 180° and 270°.
in quadrant III,
since it is between 180° and 270°.
 Since
Since  , and since
, and since  ,
we take
,
we take  , the numerator of the cosine and
, the numerator of the cosine and  ,
the denominator of the cosine, draw a perpendicular from the terminal
side of
,
the denominator of the cosine, draw a perpendicular from the terminal
side of  to the x-axis, and label the horizontal side
of the resulting triangle
to the x-axis, and label the horizontal side
of the resulting triangle  , (negative because it goes
to the left), and the hypotenuse
, (negative because it goes
to the left), and the hypotenuse  . The hypotenuse
. The hypotenuse  is
always taken positive:
is
always taken positive:
 Now we use the Pythagorean theorem to find the length of
the vertical side:
Now we use the Pythagorean theorem to find the length of
the vertical side:





 Since the vertical side of the right triangle goes
down from the x-axis, we label it negative as
Since the vertical side of the right triangle goes
down from the x-axis, we label it negative as 
 Next we want to find
Next we want to find 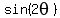 .
We use the identity:
.
We use the identity:
 We substitute
We substitute and
and 

 Edwin
Edwin