Question 348510: log(n)39870=28
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! An equation of this form:
log(expression) = 0ther-expression
is usually solved by rewriting it in exponential form. In general,  is equivalent to is equivalent to  . In your case: . In your case:

is equivalent to:

To solve this equation we want to end up with an equation of the form:
n = expression
The "n" above has no visible exponent. Nevertheless the "n" does have an exponent. Any "invisible" exponent is always understood to be a 1. So, even though we don't usually write it this way, what we are looking for is:
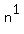 = experession. = experession.
So how to we change the 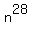 that we have into the that we have into the 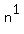 that we want? Thinking through our rules for exponents and thinking about when we get a 1 as an answer, we may be able to realize that that we want? Thinking through our rules for exponents and thinking about when we get a 1 as an answer, we may be able to realize that- the rule for exponents,
 gives us a situation where we multiply exponents, and gives us a situation where we multiply exponents, and - Multiplying reciprocals always results in 1!
So in order to change the 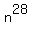 to to 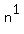 we will need to raise it to the reciprocal of 28, 1/28, power. And if we raise the left side to the 1/28 power, we must also raise the right side to the same power: we will need to raise it to the reciprocal of 28, 1/28, power. And if we raise the left side to the 1/28 power, we must also raise the right side to the same power:

which simplifies to

which, in radical form, is

This is an exact expression for the solution. If you need a decimal approximation, then we can use out calclators. If your calculator has buttons for parentheses, "(" and ")", then you can just type:
39870^(1/28)
If your calculator does not have buttons for parentheses, then first calculate 1/28 (approximately 0.0357142857) and use this decimal for the exponent:
39870^0.0357142857
Either way you should get appoximately 1.46.
|
|
|