|
Question 347597: 1.(a)given the matrix=A
{2 3},what ar its dimension
{0-1}
{1 4}
b)can these matrices be multiplied,why or why not?
{2} {3 0}
{4} {-2 3}
{0} {1 2}
Found 2 solutions by Edwin McCravy, Fombitz:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. (a) Given the matrix  , ,
what are its dimensions?
Dimensions are "down by across". It is 3 elements down
and 2 elements across. So it's a 3 by 2.
(b) Can these matrices be multiplied? Why or why not?
 No they can't, because the matrix on the left is a 3 by 1 matrix and the
matrix on the right is a 3 by 2 matrix.
You can only multiply a "p by q" matrix on the left by a "q by r" matrix
on the right and get a "p by r" matrix.
(p by q)×(q by r) = (p by r)
The "inner" dimensions q must be the same, and if so, then the product
matrix will have the "outer" dimensions, p by r. Examples:
A 6 by 5 matrix on the left can be multiplied by a 5 by 9 matrix on the right
to give a 6 by 9 matrix, because the inner dimensions are both 5 and the outer
dimensions are 6 by 9.
(6 by 5)×(5 by 9) = (6 by 9)
A 3 by 1 matrix on the left can be multiplied by a 1 by 3 matrix on the right
to give a 3 by 3 matrix, because the inner dimensions are both 1 and the outer
dimensions are 3 by 3.
(3 by 1)×(1 by 3) = (3 by 3)
A 1 by 3 matrix on the left can be multiplied by a 3 by 1 matrix on the right
to give a 1 by 1 matrix, because the inner dimensions are both 3 and the outer
dimensions are 1 by 1.
(1 by 3)×(3 by 1) = (1 by 1)
A 58 by 29 matrix on the left can be multiplied by a 29 by 73 matrix on the
right to give a 58 by 73 matrix, because the inner dimensions are both 29 and
the outer dimensions are 58 by 73.
(58 by 29)×(29 by 73) = (58 by 73)
However, in your problem (b), a 3 by 1 matrix on the left cannot be multiplied
by a 3 by 2 matrix on the right, because the inner dimensions are 1 and 3 are
they are not the same.
(3 by 1)×(3 by 2)
is not defined because the inner dimensions are not the same.
If you had been given these matrices instead:
No they can't, because the matrix on the left is a 3 by 1 matrix and the
matrix on the right is a 3 by 2 matrix.
You can only multiply a "p by q" matrix on the left by a "q by r" matrix
on the right and get a "p by r" matrix.
(p by q)×(q by r) = (p by r)
The "inner" dimensions q must be the same, and if so, then the product
matrix will have the "outer" dimensions, p by r. Examples:
A 6 by 5 matrix on the left can be multiplied by a 5 by 9 matrix on the right
to give a 6 by 9 matrix, because the inner dimensions are both 5 and the outer
dimensions are 6 by 9.
(6 by 5)×(5 by 9) = (6 by 9)
A 3 by 1 matrix on the left can be multiplied by a 1 by 3 matrix on the right
to give a 3 by 3 matrix, because the inner dimensions are both 1 and the outer
dimensions are 3 by 3.
(3 by 1)×(1 by 3) = (3 by 3)
A 1 by 3 matrix on the left can be multiplied by a 3 by 1 matrix on the right
to give a 1 by 1 matrix, because the inner dimensions are both 3 and the outer
dimensions are 1 by 1.
(1 by 3)×(3 by 1) = (1 by 1)
A 58 by 29 matrix on the left can be multiplied by a 29 by 73 matrix on the
right to give a 58 by 73 matrix, because the inner dimensions are both 29 and
the outer dimensions are 58 by 73.
(58 by 29)×(29 by 73) = (58 by 73)
However, in your problem (b), a 3 by 1 matrix on the left cannot be multiplied
by a 3 by 2 matrix on the right, because the inner dimensions are 1 and 3 are
they are not the same.
(3 by 1)×(3 by 2)
is not defined because the inner dimensions are not the same.
If you had been given these matrices instead:
 then you would have had a 1 by 3 matrix on the left to multiply by a 3 by 2
matrix on the right, and they could be multiplied because the inner dimensions
are both 3. The product matrix would be a 1 by 2 matrix because they would be
the outer dimensions.
(1 by 3)×(3 by 2) = (1 by 2)
However if you wrote the second one on the left and the first one on the right
like this:
then you would have had a 1 by 3 matrix on the left to multiply by a 3 by 2
matrix on the right, and they could be multiplied because the inner dimensions
are both 3. The product matrix would be a 1 by 2 matrix because they would be
the outer dimensions.
(1 by 3)×(3 by 2) = (1 by 2)
However if you wrote the second one on the left and the first one on the right
like this:
 you could not multiply them because the inner dimensions would not be the same:
(3 by 2)×(1 by 3 is not defined.
The commutative principle does not hold for matrix multiplication like it
holds for ordinary number multiplication.
That is when you multiply 2×3 you get 6, which is the same as when you
multiply 3×2. So the commutative principle holds for ordinary number
multiplication.
Notice this however. When you multiply
you could not multiply them because the inner dimensions would not be the same:
(3 by 2)×(1 by 3 is not defined.
The commutative principle does not hold for matrix multiplication like it
holds for ordinary number multiplication.
That is when you multiply 2×3 you get 6, which is the same as when you
multiply 3×2. So the commutative principle holds for ordinary number
multiplication.
Notice this however. When you multiply
 ,
and they can be multiplied, because
(2 by 2)×(2 by 2) = (2 by 2)
the inner dimensions are the same,
you get this 2 by 2 matrix ,
and they can be multiplied, because
(2 by 2)×(2 by 2) = (2 by 2)
the inner dimensions are the same,
you get this 2 by 2 matrix  But when you multiply
But when you multiply
 ,
and they can be multiplied, too, because
(2 by 2)×(2 by 2) = (2 by 2)
the inner dimensions are the same,
you get this 2 by 2 matrix ,
and they can be multiplied, too, because
(2 by 2)×(2 by 2) = (2 by 2)
the inner dimensions are the same,
you get this 2 by 2 matrix 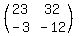 So if you reverse the order of two matrices, even if they can still be
multiplied, you don't get the same answer.
Edwin
So if you reverse the order of two matrices, even if they can still be
multiplied, you don't get the same answer.
Edwin
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) 3 x 2 (rows x columns)
.
.
.
b) No, the first is 3 x 1 and the second is 3 x 2.
The numbers of columns of the first matrix must match the number of rows of the second to allow for matrix multiplication.
|
|
|
| |