|
Question 347126: how do i factor completely M^6 - 4096?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! One of the techniques used in factoring is factoring by patterns. There are often 5 patterns that are taught. We will need three of them for this problem:- Difference of squares:
 - Difference of cubes:
 - Sum of cubes:

(Note: There ino "Sum of squares" pattern.)
Learning how to use these patterns effectively involves learning how to match your expression with one of the patterns. Part of this is understanding that the "a" and "b" in the pattern can be any expression. And part is learning how to recognize perfect squares and perfect cubes.
Recognizing numbers that are perfect squares is fairly easy. If you don't know a number to be a perfect square then ask your calculator for its square root. If the square root is a whole number then original number is a perfect square. You probably don't know if 4096 is a perfect square. But your calculator will tell you that its square root is 64. So 4096 is a perfect square:  . .
Recognizing variable expressions that are perfect squares is fairly easy. Because of how exponents work, a perfect square variable expression will have an even exponent. Some examples:




etc.
So 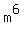 , with its even exponent, is also a perfect square. , with its even exponent, is also a perfect square.
At this point we already know that your expression fits the pattern for a difference of squares with the "a" being  and the "b" being 64. So we could start factoring now. But before doing that, let's look at recognizing perfect cubes. and the "b" being 64. So we could start factoring now. But before doing that, let's look at recognizing perfect cubes.
Recognizing numbers that are perfect cubes is not as easy as perfect squares because most people know a lot more perfect square numbers than they know perfect cube numbers. But we can still ask our calculators. To find cube roots on a calculator, raise the number to the 1/3 power. To find the cube root of 4096 use 4096^(1/3) if your calculator supports parentheses. (Use 4096^0.333333 if your calculator does not support parentheses.) You should find that 4096 is a perfect cube, too. (Earlier we found that it was 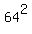 .) It is .) It is 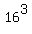 . .
Recognizing variable expressions that are perfect cubes is fairly easy. Because of how exponents work, a perfect cube variable expression will have an exponent that is divisible by 3. Some examples:




etc.
So 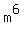 is a perfect cube since its exponent, 6, is divisible by 3. is a perfect cube since its exponent, 6, is divisible by 3.
What we have found so far is that 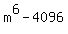 is both a difference of squares and a difference of cubes! is both a difference of squares and a difference of cubes!


So which pattern do we use? Ultimately either one can work. But I recommend, when you have a choice like this, that you use the difference of squares pattern. This is what we will do. Using the difference of squares pattern with "a" being  and "b" being 64 we get: and "b" being 64 we get:
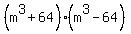
When you reduce fractions you know that you keep reducing until you cannot reduce any further. Factoring is like that, too. Keep factoring until you can't factor any further. Looking at each factor we can see that the first term,  , is clearly a perfect cube. So we have to ask ourselves, is 64 a perfect cube, too? If it is, then the first factor is a sum of cubes (for which we have a pattern) and the second factor is a difference of cubes (for which we have another pattern)! Finding 64^(1/3) (or if you know your perfect cubes better than most), you will find that , is clearly a perfect cube. So we have to ask ourselves, is 64 a perfect cube, too? If it is, then the first factor is a sum of cubes (for which we have a pattern) and the second factor is a difference of cubes (for which we have another pattern)! Finding 64^(1/3) (or if you know your perfect cubes better than most), you will find that  . So we have: . So we have:
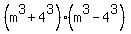
Using the sum of cubes pattern on the first factor and the difference of cubes pattern on the second factor we get:
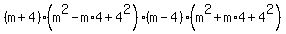
which simplifies to:
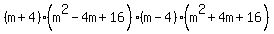
None of these factors will factor any further (no matter what factoring technique you try) so this is the final answer.
Note: If you start with the difference of cubes pattern first instead of the difference of squares you get:
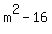
which simplifies to:
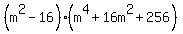
The first factor is clearly a difference of squares which can be factored. And factoring it will give you the (m+4) and (m-4) factors we found above.
The second factor will also factor but not very easily. This is why, when you have a choice between using the difference of square and difference of cubes patterns, you should choose the difference of squares pattern.
In case you're curious, here's how to factor 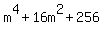 . .
First we add a strange looking zero: 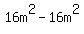 . (This is zero, right?) This gives us: . (This is zero, right?) This gives us:
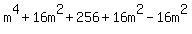
Selectively simplifying we get:
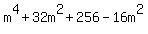
The first three terms of this match one of the "other" patterns:  or or  with "a" being with "a" being 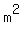 and "b" being 16. Factoring the first three terms using this pattern we get: and "b" being 16. Factoring the first three terms using this pattern we get:
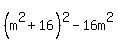
This, if you look carefully, is a difference of squares! It is 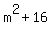 squared minus squared minus 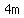 squared. So we can use the difference of squares pattern on it with the "a" being (m^2 + 16) and the "b" being 4m. Using this pattern we get: squared. So we can use the difference of squares pattern on it with the "a" being (m^2 + 16) and the "b" being 4m. Using this pattern we get:
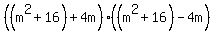
which gives us the other two factors we found above. I think you'll agree that the factoring was much more difficult this way than when we used the difference of squares first.
|
|
|
| |