SOLUTION: How do I solve for x when the area of the rectangle is 30 and the length is 3x+1 and the width is x?

Algebra ->  Rectangles -> SOLUTION: How do I solve for x when the area of the rectangle is 30 and the length is 3x+1 and the width is x?      Log On


   

Question 346436: How do I solve for x when the area of the rectangle is 30 and the length is 3x+1 and the width is x?
Found 2 solutions by mananth, ewatrrr:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!
Area of rectangle = L*W
30=(3x+1)*x
30=3x^2+x
3x^2+x-30=0
3x^2+10x-9x-90=0
3x(x+10)-9(x+10)=0
(x+10)(3x-9)=0
3(x+10)(x-3)=0
x=3

Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
Hi,
*Note: Area = length*width
The question states the following to be true:
.
(3x + 1)*x = 30
.
3x%5E2+%2B+x+=30
.
3x%5E2+%2B+x+-30=0
.
Use the quadratic formual to solve:
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
.
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 3x%5E2%2B2x%2B-30+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%282%29%5E2-4%2A3%2A-30=364.

Discriminant d=364 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-2%2B-sqrt%28+364+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%282%29%2Bsqrt%28+364+%29%29%2F2%5C3+=+2.84646400472315
x%5B2%5D+=+%28-%282%29-sqrt%28+364+%29%29%2F2%5C3+=+-3.51313067138982

Quadratic expression 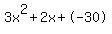3x%5E2%2B2x%2B-30 can be factored:
3x%5E2%2B2x%2B-30+=+3%28x-2.84646400472315%29%2A%28x--3.51313067138982%29
Again, the answer is: 2.84646400472315, -3.51313067138982. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+3%2Ax%5E2%2B2%2Ax%2B-30+%29