Question 3457: I have these six problems that I need to work and can't remember what to do.
1. x^2-4=0
2. x^2+x=0
3. x^2+7x+12=0
4. x^2+5x=-4
5. 3x^2+5x-10=0
6. 4x^2+3x+8=0
Found 2 solutions by drglass, AnlytcPhil:
Answer by drglass(89)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have a few options for solving these problems.
- x^2-4=0
- x^2+x=0
- x^2+7x+12=0
- x^2+5x=-4
- 3x^2+5x-10=0
- 4x^2+3x+8=0
In the first problem, you can subtract zero from both sides to get  or x = +/- 2, or or x = +/- 2, or
you can factor the problem 
In the second problem, you can factor x from the equation to get
 , this gives us x = 0 and x = -1 , this gives us x = 0 and x = -1
In this problem, you have to make some observations, first notice you can factor 12 into the following pairs ({12, 1}, (6, 2} and {4, 3}). The pair {4, 3} sum to seven, so we can factor this equation as follows:
 , therefore x = -4 and x = -7. , therefore x = -4 and x = -7.
This problem is similar to the previous problem, but first you must subtract 4 from both sides to get x^2 + 5x + 4 = 0. The common factors of 4 are ({4,1} and {2,2}). The pair {4,1} sum to 5, so we can factor this equation as follows:
 , therefore x = -1 and x = -4. , therefore x = -1 and x = -4.
This problem is a bit more complex, it requires the use of the quadratic formula for finding roots of a quadratic equation with the form  . If the roots are x1 and x2, the quadratic formula says: . If the roots are x1 and x2, the quadratic formula says:
x1 = 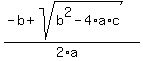 and x2 = and x2 = 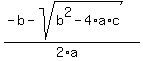
For 3x^2 + 5x - 10 = 0, a = 3, b = 5 and c = -10. This means the roots are:
x1 =  , which reduces to, x1 = , which reduces to, x1 = 
and x2 = 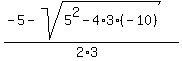 , which reduces to, x2 = , which reduces to, x2 = 
Like the previous problem, this one requires use of the quadratic equation, unfortunately, this one involves complex numbers
The equation 4x^2 + 3x + 8 = 0 gives us a = 4, b = 3 and c = 8
The roots of this equation are:
x1 = 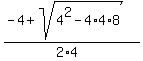 , which reduces to x1 = , which reduces to x1 = 
and x2 = 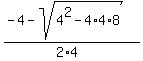 , which reduces to x2 = , which reduces to x2 = 
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have these six problems that I need to work and can't remember what to do.
1. x²-4=0
Factor the LHS as the difference of two perfect squares
(x-2)(x+2) = 0
Set each factor = 0
x-2 = 0, or x = 2
x+2 = 0, or x = -2
--------------------------------------------
2. x²+x=0
Factor the LHS by factoring out x
x(x-2)
Set each factor = 0
x=0,
x-3 = 0, or x = 3
--------------------------------------------
3. x²+7x+12=0
Factor the LHS by thinking of two positive integers that have product
12 and sum 7, they are 4 and 3.
(x+4)(x+3) = 0
Set each factor = 0
x+4 = 0, or x = 4
x+3 = 0, or x = 3
-----------------------------------
4. x²+5x=-4
Get 0 on the right by adding 4 to both sides:
x²+5x+4 = 0
Factor the LHS by thinking of two positive intergers that have product
4 and sum 5, they are 4 and 1.
(x+4)(x+3) = 0
Set each factor = 0
x+4 = 0, or x = 4
x+3 = 0, or x = 3
--------------------------------
5. 3x²+5x-10=0
That won't factor so you have to use the quadratic formula
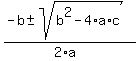
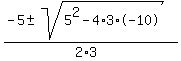
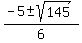
---------------------------
6. 4x²+3x+8=0
That won't factor so you have to use the quadratic formula
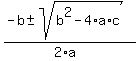


That won't factor so you have to use the quadratic formula
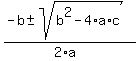
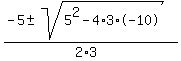
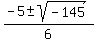
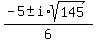
Edwin
|
|
|