SOLUTION: x³ + 5x² + 8x + 40 = 0 check all real solutions in the equation. I know how to solve the equation is by factoring but once I factor I get (x+5)(x²+8). After that I get -5 an

The square root (or any even root) of a negative number is not considered a
solution ONLY if you are considering only REAL, not IMAGINARY solutions.  But
if you are studying complex IMAGINARY numbers, then you must include them as
solutions.

Also you should not leave the imaginary solutions 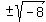 like that.
You must reduce them to their simplest radical form, like this:







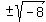
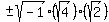
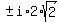
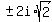A polynomial equation of degree 3 has 3 solutions (counting multiplicities
and imaginary solutions).  So the three solutions to your polynomial equation
of degree has these three solutions:

{-5, , }

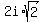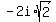Edwin