Question 344674: Hi I don't know how to solve the following :
1.e^(2lnx+lny)
2. ln square root sign(e^x+y)
3.log to the base 3 - log3 (2-3x)= log9 (6x^2-19x+2)
4. simultaneous equations :
I) log2X (log 2 to the base x) - log4y (log 4 to the base y ) =4
and log2(x-2y)(log 2 to the base x-2y)=5
Found 2 solutions by stanbon, jsmallt9:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! 1.e^(2lnx+lny)
= e^(ln(x^2)+ln(y)
---
= e^(ln(x^2*y))
---
= x^2*y
====================
2. ln square root sign(e^x+y)
---
= ln[e^(x+y)]^(1/2)
---
= (1/2)*ln(e^(x+y))
---
= (1/2)(x+y)
====================
3.log to the base 3 - log3 (2-3x)= log9 (6x^2-19x+2)
Something is missing in your problem statement.
================================================
4. simultaneous equations :
I) log2X (log 2 to the base x) - log4y (log 4 to the base y ) =4
and log2(x-2y)(log 2 to the base x-2y)=5
---
log2(x)-log2(y) = 4
log2(x-2y) = 5
------
log2(x/y) = 4
log2(x-2y) = 5
-------
x/y = 2^4
x-2y = 2^5
-------
x -16y = 0
x -2y = 32
-----
Subtract 1st from 2nd and solve for "y":
14y = 32
y = 16/7
----
Since x/y = 16
x = 16y = 16(16/7) = 16^2/7
--------
Solution: x = 16/7 ; y = 16^2/7
====================================
Cheers,
Stan H.
=================
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website! The key to the first two problems is to understand that any expression of the form  or  can be simplified easily because of the fact that exponentiation of e and ln's are inverses of each other. So if we can transform an expression into the form or the rest of the problem will be simple.
We want to transform 2ln(x)+ln(y) into a single logarithm, if possible. Fortunately we have a property,  , which allows us to move a coefficient, like our 2, into the argument as an exponent:
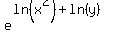
And we have another property of logarithms,  , which allows us to combine the sum of two logarithms (of the same base) into one:
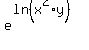
We now have the desired form. Since  represents the exponent for e which results in 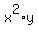 and since it is the exponent for e in this expression,  (Alternate explanation: Since exponentiating e and ln's are inverses,  for all expressions for p.)
2. I'm assuming the problem is
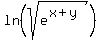
If so, please use parentheses on multiple term exponents:
ln square root sign(e^(x+y))
Again we want to transform this into the form: .
We need to get rid of the square root. To do this we first need to remember that radicals can be replaced with an appropriate fractional exponent. For square roots the fractional exponent is 1/2:
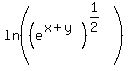
We can simplify the argument by using the exponent rule for raising a power to a power: Multiply the exponents:
We now have the desired form. And, with logic like that used in #1, this simplifies to:
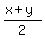
3. I assume the problem is to solve:
Solving equations where the variable is in the argument (or base) of one or more logarithms usually involves transforming the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)
It may seem that we already have the second form. But the second form requires that the two logarithms have the same base. So we need to change the base 3 log into a base 9 log or vice versa or change both logs into a 3rd base (perhaps base 10 or base e so we could use our calculators).
For this equation since 9 is a power of 3 (and vice versa) we will change one base into the other. And for this we will use the change of base formula for logarithms:  We will use this to change
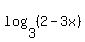
into
Since 3 is the square root of 9 and since 1/2 is the exponent for square roots, the denominator simplifies to 1/2:
Multiplying the top and bottom of the "big" fraction by 2 we get:
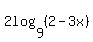
So now the equation is:
We have one more step to achieve the desired form. We need to eliminate the 2 in front of the first log. Fortunately we can use again:
This is the desired form. With this form we use the logic: If the logarithms (exponents) for two expressions are equal, then the expressions are equal. This gives us:
This is a quadratifc equation we can solve. First we'll simplify the left side (i.e. square 2-3x):
Make one side zero (by subtracting the entire right side from both sides):
Then we factor (or use the Quadratic Formula):
Now we use the Zero Product property which tells us that this (or any) product can be zero only if one (or more) of the factors is zero. So
3x + 1 = 0 or x + 2 = 0
Solving these we get:
x = -1/3 or x = -2
With logarithmic equations it is important, not just a good idea, to check your answers. You must make sure that no argument of any logarithm becomes zero or negative. Any "solutions" that make a logarithm's argument zero or negative must be rejected! (Be sure to check with the original equation!)
Checking x = -1/3:
At this point we can stop because we can see that we have nothing but the sum of positive numbers in each argument so the final arguments will work out positive.
Checking x = -2:
At this point we can stop because we can see that we have nothing but the sum of positive numbers in each argument so the final arguments will work out positive.
Both solutions check so we have two solutions to this problem.
4. For 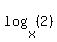 please use language like:
(base x log of 2)
and for 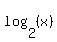 please use language like:
(base 2 log of x)
It is very hard to understand the way you have been trying to describe your problems.
I assume the problem is supposed to be:
With the first equation we will use the same technique as problem #3: Change the base first and go from there:
Now we can use yet another property of logarithms,  , to combine the two logarithms into one:
Our system is now:
Both equations are of the form:
log(expression) = expression
With this form the next step is to rewrite the equation in exponential form. In general
 can be rewritten as  . Using this on both equations of our system we get:
Simplifying the left sides we get:
To solve this system we can use the Substituion Method. We can quickly solve the second equation for x by adding 2y to each side:
x = 2y + 32
Then we can substitute for x in the first equation:
Multiplying both sides by y eliminates the fraction:
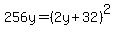
Simplifying the right side we get:
Now we want one side to be zero (so we subtract 256y from each side):
Factor. First the GCF:
Then factor the trinomial:
Then the Zero Product Property:
y - 16 = 0
Solve:
y = 16
Find x using x = 2y+32:
x = 2(16) + 32 = 32 + 32 = 64
Check using the orginal equations:
Since x and y are both positive we can see that the arguments of both logarithms in the first equation will be positive, too. Now we check the second equation:
Check! So the solution to the system is (64, 16).
In the future please post no more than 2 problems within at a time. The more you include in a single post, the less likely it will be that you will get a tutor to volunteer to respond.
|
|
|
