Question 342339: Ava rode her bike from her house to her friends house averaging 16 km per hour. It turned dark so her friend drove her home at a rate of 80 km per hour. If Ava's total traveling time was 3 hours, how far away did her friend live?
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! The formula we will use is R * T = D where R = rate of speed in km/hr, T = time in hr, and D = distance in km.
We let T = total time it took to get there and back.
We let D = total distance from there and back.
Going to her friend's house, we let x = the amount of time it took, and we let D/2 = the distance she traveled, and we let 16 = the rate of her speed.
The formula for her going is 16 * x = D/2.
Coming back from her friend's house, we let T-x = the amount of time it took, and we let D/2 = the distance she traveled, and we let 80 = the rate of her speed in her friend's car.
The formula for her coming back is 80 * (T-x) = D/2.
Both of these formulas are equal to D/2, so they are both equal to each other.
We get:
16 * x = 80 * (T - x)
We expand these formulas by removing parentheses to get:
16 * x = 80 * T - 80*x
We add 80*x to both sides of this equation to get:
16*x + 80*x = 80*T
We combine like terms to get:
96*x = 80*T
We know that T = 3 hours because that's what we were given.
Our formula becomes:
96*x = 80 * 3
This becomes 96 * x = 240
We divide both sides of this equation by 96 to get:
x = 240/96 which makes x = 2.5 hrs.
Since T is equal to x + (T-x), then (T-x) has to be .5 hrs.
Now that we know x and T-x, we can solve for D/2.
In the formula where Ava goes to her friend's house, we get:
16 * x = D/2 becoming 16 * 2.5 = D/2 which makes D/2 equal to 40 km.
In the formula where Ava comes back from her friend's house, we get:
80 * (T-x) = D/2 becoming 80 * .5 = D/2 which makes D/2 equal to 40 km.
Both formulas point to the same distance as they should.
The distance from Ava'a house to her friend's house is equal to 40 km.
40 km = D/2
D is the distance there and back.
D is therefore equal to 80 km.
But you didn't want D.
You wanted D/2 which is the distance from Ava's hour to her friend's house.
Your answer is therefore equal to 40 km.
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ava rode her bike from her house to her friends house averaging 16 km per hour. It turned dark so her friend drove her home at a rate of 80 km per hour. If Ava's total traveling time was 3 hours, how far away did her friend live?
For this problem, we need to reealize that since the total time for the roundtrip was 3 hours, then time to travel to her friend's house, plus time to return home equals 3. Using D as the distance, the speed to the friend's house, and the speed on the return trip, this is expressed as:

Multiplying the equation by its LCD, 80, we get:
5D + D = 240
6D = 240
D, or distance to friend's house = 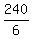 or or  kilometers. kilometers.
|
|
|