|
Question 342243: The sum of the measures of two complementary angles exceeds the difference of the measures of their supplements by 32 degrees. Find the measure of each angle.
Found 2 solutions by mananth, MathTherapy:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! let one angle be x
the other complementary angle will be 90-x
...
supplementary angle will be 180-x
..
x+(90-x)-x+(180-x)= 32
x+90-x -x +180 -x=32
-2x=32-180-90
-2x=-238
divide by -2
x= -238/-2
x=119 degrees
CHECK
119+(90-119)-119+(180-119)=32
Answer by MathTherapy(10556)  (Show Source):
You can put this solution on YOUR website! The sum of the measures of two complementary angles exceeds the difference of the measures of their supplements by 32 degrees. Find the measure of each angle.
Let the 1st angle be A, then the 2nd angle or the complement of the 1st angle = 90 A
The supplement of the 1st angle would then be 180 A, and the supplement of the 2nd angle = 180 (90 A), or 180 90 + A, or 90 + A
Now, since the sum of the measures of the two complementary angles exceeds the difference of the measures of their supplements by 32 degrees, then well have:
A + 90 A = 180 A (90 + A) + 32
90 = 180 A 90 A + 32
90 = 122 2A
2A = 122 90___2A = 32
A, or 1st angle = 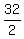 =  , and the measure of the 2nd angle = 90 16, or 
-----------
Check
-----------
The sum of the complement angles or 90 (16 + 74), exceeds the difference of their complements, 164 (180 - 16) and 106 (180 - 74) or 58 (164 - 106) by 32.
Send comments and thank-yous to MathMadEzy@aol.com
|
|
|
| |
