Question 341432: Maximize 5x + 3y
Subject to the constraints
5x + 2y <= 40
3x + 6y <= 48
x <= 7
2x - y >= 3
x,y >= 0
Graph the following equation
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Determine the feasible region by plotting the constraint equations.
Find the intersection points.
Between the x-axis and 
( , )
The other intersection point is ( ,).
Find the intersection points of  and 
(, )
Find the intersection point between
1.
2. 
From eq. 2,
Substitute into eq. 1,
Then from eq. 2,
( , )
Finally find the intersection point between and
Substitute,
Then
( , )
.
.
.
.
.
.
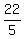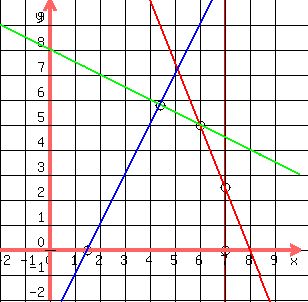
The maximum and minimum of the function occurs at one of these vertices.
(,) :
(,):
(,):
(,):
(,):
.
.
.
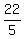The maximum value is  and occurs at (,).
|
|
|
