SOLUTION: Find the cube roots of -i.

i written as a complex number of the form a+bi is 0+1i.
The complex number a+bi is the vector that goes from the
origin to the point (a,b).

Therefore the number 0+1i is the vector that goes from the
origin to the point (0,1)

We want to put that number in trigonometric form.

First we draw the vector 0+1i which goes from the origin to 
the point (0,1)

 

and we see that its angle with the right hand side of the
x-axis is 90°:



So we see that the vector's magnitude (length) is r=1, and
its angle is 

Therefore the trigonometric form of i, or 0+1i, is

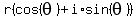 or in this case



Now the cosine and sine will not change if we add or subtract 360° 
any whole number of times.  So we can write that as:



Next we use DeMoivre's theorem, which states that



with , , , since the cube root
is the  power.







Now we substitute any three consecutive values of integer n
We use the easiest ones, 0, 1 and 2

Substituting n=0






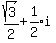Substituting n=1






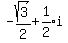Substituting n=2








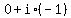
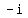So the three cube roots of i are

, , 

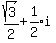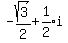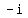Edwin