Question 34042: Use the geometric sequence of numbers 1, 1/2, 1/4, 1/8,…to find the following:
What is r, the ratio between 2 consecutive terms?
Using the formula for the sum of the first n terms of a geometric series, what is the sum of the first 10 terms? Please round your answer to 4 decimals.
Using the formula for the sum of the first n terms of a geometric series, what is the sum of the first 12 terms? Please round your answer to 4 decimals.
What observation can make about these sums? In particular, what number does it appear that the sum will always be smaller than?
What do you think? I need help, :')
Answer by xcentaur(357)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1, 1/2, 1/4, 1/8,…
What is r, the ratio between 2 consecutive terms?
second term=1/2
third term=1/4
ratio r=third/second=(1/4)/(1/2)=(1/2)
Using the formula for the sum of the first n terms of a geometric series, what is the sum of the first 10 terms? Please round your answer to 4 decimals.
a=1,n=10,r=0.5
sum for n terms=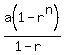
=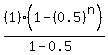
=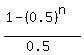
=
=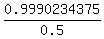
=1.998046875
=1.9980(rounding off)
Using the formula for the sum of the first n terms of a geometric series, what is the sum of the first 12 terms? Please round your answer to 4 decimals.
a=1,n=12,r=0.5
sum for n terms=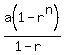
=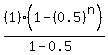
=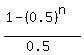
=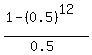
=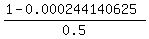
=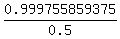
=1.99951171875
=1.9995(rounding off)
What observation can make about these sums? In particular, what number does it appear that the sum will always be smaller than?
The number will approach 2.
It will reach 1.999999999999999999999999....upto infinity, but it will always be smaller than 2
Hope this helps,
-xC
|
|
|