Question 340247: I am asked to express in terms of log m and log n
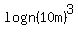
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! I could interpret this in 2 ways.
The first way would be:
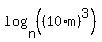
Under that assumption, your answer would be:
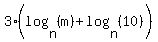
The second way would be:
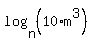
Under that assumption, your answer would be:
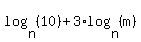
The difference is in whether you are taking 10 * m and then raising the result to the 3d power, or you are taking m to the third power and then multiplying the result by 10.
There are two main concepts at work.
The first concept is that  .
The second concept is that  .
If you are solving for  , then you use the first concept because the letter a represents 10 and the letter b represents m^3.
If you are solving for 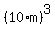 , then you use the second concept because
the letter a represents (10*m) and the letter b represents 3.
Note that the concept used for each piece of the puzzle changes as you progress through the steps of the problem.
log(10*m^3) becomes log(10) + log(m^3) because a represents 10 and b represents m^3. The first concept was used.
now that you have log(10) + log(m^3), then the second part of log(m^3) becomes 3*log(m) because a represents m and b represents 3). The second concept was used on the second part.
The first concept was used to break it up into 2 pieces.
The second concept was used to break the second piece down further.
The log of (10 * m^3) is not the same as the log of ((10*m)^3).
The base used was not important to the solution because the same concepts apply regardless of the base.
If you assume n is 10, then you can solve for any m using the calculator.
If you assume n is the natural log to the base e, then you can solve for any m using the calculator.
If n is any number other than 10 or e, then you would need to use the conversion formula to solve using your calculator.
To do that, you would do the following:
Assume log of m to the base n.
Take the log of m to the base 10 and divide it by the log of n to the base 10.
You will get the same answer.
An easy example:
Log of 8 to the base 2 = 3 because 2^3 = 8.
To solve this using your calculator, you would take the log of 8 to the base 10 and divide that by the log of 2 to the base 10.
Using your calculator, you would get LOG(8) / LOG(2) = 3.
When you use your calculator, the LOG function implies the base of 10.
Similarly, when you use your calculator, the LN function implies the base of e.
You could also have done LN(8) / LN(2) and gotten the same answer of 3.
You can convert the log of any base to the log of any other base by using the conversion formula of:
|
|
|
