SOLUTION: 1. if it takes john 900 seconds to run 1 mile then he is running at a rate of 4 mph. show work 2. Three consecutive odd counting numbers have the property that the sum of the lar

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: 1. if it takes john 900 seconds to run 1 mile then he is running at a rate of 4 mph. show work 2. Three consecutive odd counting numbers have the property that the sum of the lar      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 338228: 1. if it takes john 900 seconds to run 1 mile then he is running at a rate of 4 mph.
show work
2. Three consecutive odd counting numbers have the property that the sum of the largest and twice the smallest is 64. what is the middle number.
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Only one question per post. Which one do you want us to do? Don't write to me, repost.

John

My calculator said it, I believe it, that settles it

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
1. if it takes john 900 seconds to run 1 mile then he is running at a rate of 4 mph.
show work

1mi%2F900sec%22%D7%22%2860sec%29%2F%281min%29%22%D7%22%2860min%29%2F%281hr%29

Cancel the seconds:

1mi%2F900cross%28sec%29%22%D7%22%2860cross%28sec%29%29%2F%281min%29%22%D7%22%2860min%29%2F%281hr%29

Cancel the minutes:

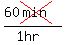1mi%2F900cross%28sec%29%22%D7%22%2860cross%28sec%29%29%2F%281cross%28min%29%29%22%D7%22%2860cross%28min%29%29%2F%281hr%29

All that's left is

%28mi%2A60%2A60%29%2F%28900hr%29

%283600mi%29%2F%28900hr%29

4mi%2Fhr

4expr%28mi%2Fhr%29

2. Three consecutive odd counting numbers have the property that the sum of the largest and twice the smallest is 64. what is the middle number.

Smallest of the three consecutive odd integers = n
Middle of the three consecutive odd integers = (n+2)
Largest of the three consecutive odd integers = (n+4)

largest + 2*smallest = 64

         (n+4) + 2*n = 64

         n + 4 + 2n  = 64

              3n + 4 = 64

                  3n = 60

                   n = 20

But 20 is even, not odd.  If the problem had asked for three consecutive
even counting numbers, they would be

Smallest = n = 20
Middle = (n+2) = 20+2 = 22
Largest = (n+4) = 20+4 = 24

The largest, 24 plus twice the smallest, 2*20 or 40, is 64, since 24+40 = 64.
But they're even, not odd.

Thus, there is no solution, since they must be odd.  Only such even
consecutive counting numbers exist, but no odd ones. 

Edwin