|
Question 336788: Hi, I am Kimberly,
I am in accelerated math 1 and I am getting confused with some slope problems. My teacher gave me some question and this is how she gave them give the equation, through (1,-6) slope=3 I don't know if she is meaning y intercept or slope intercept form. the answer I got was y= 3x-9 is that right?????? Then, I am gonna list a few problems, but I just need step by step so I can get it. please help.
3. find equation- vertical line thru ( 0, -3)
4. find equation- thru (-3,6)and (1,-2)
5. find equation- horizontal line thru (0,2)
7. find equation - slope= -3 and y intercept 3
10. find equation- thru ( -2, -3) and perpendicular to 3x-5y=1
I have other questions,b ut I want to see if I can get them after these. Please use step bye step so I can learn. Thanks ^_^
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! question and this is how she gave them give the equation, through (1,-6) slope=3
Use the point/slope form: y - y1 = m(x - x1)
In this problem: x1=1; y1=-6; m=3
y -(-6) = 3(x - 1)
y + 6 = 3x - 3
y = 3x - 3 - 6
y = 3x - 9; (now it is the slope intercept form)
:
You can prove this: replace x with 1, find y
y = 3(1) - 9
y = 3 - 9
y = -6, which is the value given for y
:
:
3. find equation- vertical line thru ( 0, -3)
this vertical line goes thru 0 and all values for y. therefore
x = 0 is the equation
:
4. find equation- thru (-3,6)and (1,-2)
Find the slope using the slope equation: m = 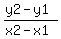
assign the given values as follows
x1=-3; y1=6
x2=1; y2=-2
m = 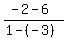 = = 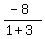 = = 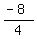 = -2 is the slope = -2 is the slope
Use the point/slope form again:
y - 6 = -2(x - (-3))
y - 6 = -2(x + 3)
y - 6 = -2x - 6
y = -2x - 6 + 6
y = -2x , is the equation
Here again, you can confirm this, replace x with -3, find the y value
:
:
5. find equation- horizontal line thru (0,2)
this horizontal line goes thru 2, and all values of x, therefore
y = 2
:
;
7. find equation - slope= -3 and y intercept 3
Here you can just substitute in the slope intercept form; y = mx + b
y = -3x + 3
;
:
10. find equation- thru ( -2, -3) and perpendicular to 3x-5y=1
First we have to find the slope of the equation,
put it in the slope intercept form
3x - 5y = 1
-5y = -3x + 1
y has to be positive, multiply by -1 to change the signs
5y = 3x - 1
Divide by 5
y =  x - x - 
then slope: m1 = 
:
The relationship between the slopes of perpendicular lines is: m1*m2 = -1
 *m2 = -1 *m2 = -1
m2 =  is the slope of the perpendicular line is the slope of the perpendicular line
Find the equation for the line where: m= ; x1=-2; y1=-3 ; x1=-2; y1=-3
y -(-3) =  (x - (-2)) (x - (-2))
y + 3 =  (x + 2) (x + 2)
y + 3 =  x - x - 
y =  x - x -  - 3 - 3
y =  x - x -  - - 
y =  x - x - 
In standard form, multiply by 3
3y = -5x - 19
5x + 3y = -19 is perpendicular to 3x - 5y = 1, goes thru x/y; -2,-3
:
|
|
|
| |