Question 336715: a. 1, 3, 5, 7, 9
b. 0, 50, 100, 150, 200
c. 3, 6, 12, 24, 48
d. 10, 100, 1,000, 10,000, 100,000
e. 9, 13, 17, 21, 25, 29
f. 1, 8, 27, 64, 125
Find the 100th term and the nth term for each of the
sequences in exercise 2.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a. 1, 3, 5, 7, 9
That's an arithmetic sequence with first term  and
common difference and
common difference  , because you always ADD 2 to get the next term.
So we use , because you always ADD 2 to get the next term.
So we use 




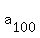  ------------------------------------
b. 0, 50, 100, 150, 200
That's an arithmetic sequence with first term
------------------------------------
b. 0, 50, 100, 150, 200
That's an arithmetic sequence with first term  and
common difference and
common difference  , because you always ADD 50 to get the next term.
That one is done exactly like problem a. I'll let you do that one
by yourself.
------------------------------------
c. 3, 6, 12, 24, 48
That's a geometric sequence with first term , because you always ADD 50 to get the next term.
That one is done exactly like problem a. I'll let you do that one
by yourself.
------------------------------------
c. 3, 6, 12, 24, 48
That's a geometric sequence with first term  and common
ration and common
ration  , because you always MULTIPLY BY 2 to get the next term.
So we use , because you always MULTIPLY BY 2 to get the next term.
So we use 

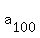  ------------------------------------
d. 10, 100, 1,000, 10,000, 100,000
That's a geometric sequence with first term
------------------------------------
d. 10, 100, 1,000, 10,000, 100,000
That's a geometric sequence with first term  and common
ratio and common
ratio  , because you always MULTIPLY BY 10 to get the next term.
That one is done exactly like problem c. I'll let you do that one
by yourself.
------------------------------------
e. 9, 13, 17, 21, 25, 29
That's an arithmetic sequence with first term , because you always MULTIPLY BY 10 to get the next term.
That one is done exactly like problem c. I'll let you do that one
by yourself.
------------------------------------
e. 9, 13, 17, 21, 25, 29
That's an arithmetic sequence with first term  and and  ,
because you always ADD 4 to get the next term.
That one is done exactly like problem a. I'll let you do that one
by yourself.
------------------------------------
f. 1, 8, 27, 64, 125
Now that one is different from the others because it is neither an
arithmetic sequence nor a geometric sequence. However we can recognize it
as the sequence of the cube of the successive positive integers.
1=1³, 8=2³, 27=3³, 64=4³, 125=5³
So ,
because you always ADD 4 to get the next term.
That one is done exactly like problem a. I'll let you do that one
by yourself.
------------------------------------
f. 1, 8, 27, 64, 125
Now that one is different from the others because it is neither an
arithmetic sequence nor a geometric sequence. However we can recognize it
as the sequence of the cube of the successive positive integers.
1=1³, 8=2³, 27=3³, 64=4³, 125=5³
So

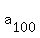  ------------------------------------
Edwin
------------------------------------
Edwin
|
|
|