|
Question 33664This question is from textbook Algebra 2 An Integrated Approach
: Find the asymptotes of the hyperbola. Then sketch its graph.
35. 
I have spent well over an hour attempting to solve this problem, and have had others try to help me with no succes. There is the answer in the back of the book, but i still want to know how to solve the problem. I hope that you will be able to help me, and tell me where I have gone wrong.
Tried methods
1) multiply 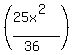 by 36 to get rid of 36 in the denominator, and then multiply the other side of the equation by 36,  I then added the  section over to the other side of the equation. Then I divided both sides by 25 
I know the Standard Equation for a hyperbola is  for horizontal and  for vertical. After that I am somewhat lost...
This question is from textbook Algebra 2 An Integrated Approach
Answer by venugopalramana(3286)   (Show Source):
You can put this solution on YOUR website! KEEP YOUR OBJECTIVE CLEAR.....
Find the asymptotes of the hyperbola. Then sketch its graph.
35.
I have spent well over an hour attempting to solve this problem, and have had others try to help me with no succes. There is the answer in the back of the book, but i still want to know how to solve the problem. I hope that you will be able to help me, and tell me where I have gone wrong.
SEE MY COMMENTS BELOW AND THE EXAMPLE AT THE END.
Tried methods
1) multiply 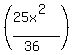by 36 to get rid of 36 in the denominator, and then multiply the other side of the equation by 36, I then added the section over to the other side of the equation. Then I divided both sides by 25
YOU ARE MISSING THE KEY POINT...SEE BELOW
--------------------------------------------------------------------------------
I know the Standard Equation for a hyperbola is for horizontal and for vertical. After that I am somewhat lost...
THIS IS THE KEY..TRY TO GET THE EQN.IN THIS FORM
SEND 25 TO THE DENOMINATOR.THAT IS ALL...THAT IS
X^2/(36/25) - Y^2/(121)=1...SO A^2=36/25...OR...A=6/5 AND B^2=121...OR...B=11
OK BUT WE WANT ASYMPTOTES..SO...
--------------------------------------------------------------------------------
SEE THE FOLLOWING EXAMPLES TO KNOW THE METHOD.AND FINALLY ANSWER FOR YOUR PROBLEM AT THE END.
--------------------------------------------------------------------------
Quadratic-relations-and-conic-sections/28184: What is the vertices, foci, and slope of the asymptotes for the hyperbola whose equation is, y^2/16 - x^2/25 =25?
SEE THE FOLLOWING AND YOU SHOULD BE ABLE TO SOLVE YOUR PROBLEM BY YOUR SELF.....
THE ANSWERS FOR YOUR CASE...H=0...K=0..A=4...B=5....EQN IS OF THE TYPE
(Y-K)^2/B^2-(X-H)^2/A^2=1....
SO VERTICES ARE...(H,(K-B)) AND (H,(K+B)) ...(0,-5) AND (0,5)
FOCI ARE {H,(K-BE)} AND {H,(K+BE)}...WHERE E IS
ECCENTRICITY =SQRT{(A^2+B^2)/B^2}=SQRT((16+25)/25)=SQRT(41/25)
SO FOCI ARE =(0,-5SQRT(41/25) AND (0,5SQRT(41/25)...
OR....(0,-SQRT(41)) AND (0,SQRT(41)
ASYMPTOTES ARE GIVEN BY
Y^2/16-X^2/25=K
25Y^2-16X^2-400K=0
(5Y+4X+A)(5Y-4X+B)=0
SLOPES OF ASYMPTOTES ARE
-4/5 AND 4/5
THE GRAPHS LOOK LIKE THIS
graph( 600, 600, -10, 10, -10, 10, 4*(1+x^2/25)^0.5,-4*(1+x^2/25)^0.5,4*x/5,-4*x/5 )
------------------------------------------
What is the vertices, foci, and slope of the asymptote for the hyperbola whose equation is, y^2 - 4x^2 - 2y - 16x + 1 = 0?
(Y^2-2*Y*1+1^2)-{(2X)^2+2*(2X)*4+4^2}-1^2+4^2+1=0
(Y-1)^2-(2X+4)^2=-16
4(X+2)^2-(Y-1)^2=16
{4(X+2)^2}/16-{(Y-1)^2}/16=1
(X+2)^2/2^2-(Y-1)^2/4^2=1...
COMPARING WITH STANDARD EQN.
(X-H)^2/A^2-(Y-K)^2/B^2=1....WE HAVE
VERTICES ARE {(H-A),K} AND {(H+A),K}=(-2-2,1) AND (-2+2,1)=(-4,1) AND (0,1)
FOCI ARE {(H-AE),K} AND {(H+AE),K}...WHERE E IS
ECCENTRICITY =SQRT{(A^2+B^2)/A^2}=SQRT((4+16)/4)=SQRT(5)
SO FOCI ARE =(-2-2SQRT(5),1) AND (-2+2SQRT(5),1)
SLOPE OF ASYMPTOTE IS GIVEN BY DIFFERENTIATION.HAVE YOU BEEN TAUGHT?PLEASE INFORM.I SHALL COME BACK ON HEARING FROM YOU.
or you can take this proposition as proved formula
the pair of asymptotes for a conic is given by the same equation as the conic except for the constant term which has to be found using the condition for the equation to represent a pair of straight lines.
HENCE EQN OF ASYMPTOTES IS GIVEN BY
y^2 - 4x^2 - 2y - 16x + K=0 , WHERE K IS DETERMINED using the condition for the equation to represent a pair of straight lines.
SINCE WE ARE TO FIND ONLY SLOPES ,WE NEED NOT DETERMINE THE CONSTANT BUT ASSUME THAT THIS EQN REPRESENTS A PAIR OF STRAIGHT LINES.SO
y^2 - 4x^2 - 2y - 16x + K=0 = (Y+2X+A)(Y-2X+B)
HENCE SLOPES ARE +2 AND -2
graph( 600, 600, -10, 10, -10, 10, 1-2*((x+2)^2-4)^0.5,1+2*((x+2)^2-4)^0.5,2x+5,-2x-3 )
-----------------------------------------------------------------------------
UNDERSTOOD THE METHOD?WE HAVE TO WRITE THE QUADRATIC IN TO 2 LINEAR FACTORS
THE EQN.IS....
X^2/(36/25) - Y^2/(121)=1 SO EQN.OF ASYMPTOTES IS
X^2/(36/25) - Y^2/(121)=K...BUT K=0 SINCE THE ASYMPTOTES PASS THROUGH THE CENTRE OF HYPERBOLA WHICH IS ORIGIN IN THIS CASE.
SO WE GET
[{X/(6/5)} + {Y/11}]=0
HENCE THE 2 ASYMPTOTES ARE...
{X/(6/5)} + {Y/11}=0 AND {X/(6/5)}-{Y/11}=0
MULTIPLYING BY LCM...66...
55X+6Y=0......AND......55X-6Y=0
OK.....IF STILL IN DOUBT PLEASE COME BACK
|
|
|
| |
