SOLUTION: Write the given expression f(x)= x^2+10x+7 in the form f(x)=a(x-h)^2+k. And identify the vertex

Algebra ->  Expressions-with-variables -> SOLUTION: Write the given expression f(x)= x^2+10x+7 in the form f(x)=a(x-h)^2+k. And identify the vertex      Log On


   

Question 335938: Write the given expression f(x)= x^2+10x+7 in the form f(x)=a(x-h)^2+k. And identify the vertex
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

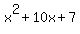x%5E2%2B10x%2B7 Start with the given expression.


Take half of the x coefficient 10 to get 5. In other words, %281%2F2%29%2810%29=5.


Now square 5 to get 25. In other words, %285%29%5E2=%285%29%285%29=25


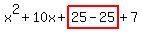x%5E2%2B10x%2Bhighlight%2825-25%29%2B7 Now add and subtract 25. Make sure to place this after the "x" term. Notice how 25-25=0. So the expression is not changed.


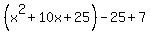%28x%5E2%2B10x%2B25%29-25%2B7 Group the first three terms.


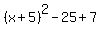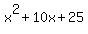%28x%2B5%29%5E2-25%2B7 Factor x%5E2%2B10x%2B25 to get %28x%2B5%29%5E2.


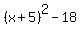%28x%2B5%29%5E2-18 Combine like terms.


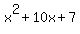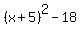So after completing the square, x%5E2%2B10x%2B7 transforms to %28x%2B5%29%5E2-18. So x%5E2%2B10x%2B7=%28x%2B5%29%5E2-18.


This means that f%28x%29=x%5E2%2B10x%2B7 is equivalent to f%28x%29=%28x%2B5%29%5E2-18.


So the equation f%28x%29=%28x%2B5%29%5E2-18 is now in vertex form f%28x%29=a%28x-h%29%5E2%2Bk where a=1, h=-5, and k=-18


Remember, the vertex of f%28x%29=a%28x-h%29%5E2%2Bk is (h,k).


So the vertex of f%28x%29=%28x%2B5%29%5E2-18 is (-5,-18) since h=-5 and k=-18


This means that the vertex of f%28x%29=x%5E2%2B10x%2B7 is (-5,-18)


If you need more help, email me at jim_thompson5910@hotmail.com

Also, feel free to check out my website.

Jim