SOLUTION: the sum of the first nine terms of an arithmetic progression is 75 and the twenty-fifth is also 75. find the common difference and the sum of the first hundred terms.

Algebra ->  Sequences-and-series -> SOLUTION: the sum of the first nine terms of an arithmetic progression is 75 and the twenty-fifth is also 75. find the common difference and the sum of the first hundred terms.      Log On


   

Question 33525: the sum of the first nine terms of an arithmetic progression is 75 and the twenty-fifth is also 75. find the common difference and the sum of the first hundred terms.
Answer by longjonsilver(2297) About Me  (Show Source):
You can put this solution on YOUR website!
25th term is a+24d, so a+24d = 75 --eqn1

Sum of 9 = 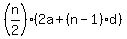+%28n%2F2%29%282a+%2B+%28n-1%29d%29+
+%289%2F2%29%282a+%2B+%289-1%29d%29+=+75+
+9%282a+%2B+8d%29+=+150+
+18a+%2B+72d+=+150+
Scale eqn1 by 3 to give 3a+72d = 225. So we have

3a+72d = 225
18a+72d = 150

Subtract, to give -15a = 75
--> a = -5

So, from a+24d = 75 we get
-5+24d = 75
24d = 80
d = 80/24
d = 10/3

This is:
-5, -5/3, 5/3, 5, 25/3, 35/3, 15, 55/3, 65/3,... which does add up to 75.

So, Sum of 100 terms is 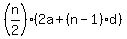+%28n%2F2%29%282a+%2B+%28n-1%29d%29+
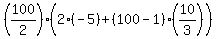
+%28100%2F2%29%282%28-5%29+%2B+%28100-1%29%2810%2F3%29%29+
+50%28-10+%2B+%2899%29%2810%2F3%29%29+
50(-10 + 330)
50(320)
50(320)
16000

jon.