Question 335193: What is the range of the inverse function of h(x) = ln (x + square root of the quantity (x squared - 1)?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
In order to find the range of h(x) we will find the domain first. The domain is the set of all possible values for the independent variable (usually this is "x").
When finding domains you start by assuming that x can be any real number. Then you determine if there are values to exclude. The most common reasons to exclude numbers from the domain are:- Values for x that would make a denominator zero.
- Values for x that would make a radicand of an even-numbered root negative. (A radicand is the expression within a radical. And even-numbered roots are 2nd roots (aka square roots), 4th roots, 6th roots, etc.)
- Values for x that would make the argument of a logarithm non-positive (i.e. zero or negative).
h(x) has no denominators. But it does have both a square root and a logarithm. So we have to ensure that the domain includes only the numbers that the argument of the logarithm positive and make the radicand zero or positive.
Let's look at the square root first. We want
Solving this quadratic inequality algebraically we start by factoring:
I hope you can see that the x values that make the product zero would be 1 and -1. For the x values that make the product positive (i.e. greater than zero) we have to think of how multiplication works. In order for the product of two numbers to be positive, then both numbers must be positive or both numbers must be negative. With some work/thought we can find that if x > 1 then both (x+1) and (x-1) are positive and that if x < -1 then both factors are negative. Combining the x values that make the radicand positive and the x values that make the radicand zero we get:
 or 
Now we will look at the logarithm. We must ensure that all numbers in the domain make the argument of the logarithm positive. Our domain up to now is:
or
The argument of the logarithm is:
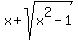
For we can see that x is positive for all these x's. Since square roots are always positive, the argument is the sum of two positive numbers. Since the sum of two positive numbers is always positive, the argument is positive if .
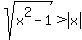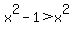For we can see that x is negative for all these x's. Since square roots are (still) always positive, the argument is the sum of a negative and a positive number. We want this sum to be positive. The only way for the sum of a negative and a positive to be positive is if the positive is greater than the absolute value of the negative. So we need  . If we square both sides of this we get:  . Subtracting  from each side we get: -1 > 0. This is a false statement. 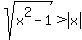This tells us that there is no solution to . And if there is no solution to 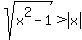, then when the argument of the logarithm can never be positive. So we must exclude these values, , from the domain!
We finally have the domain for h(x). It is .
Now we can determine the range. The lowest possible value for x is 1. For h(1) we get ln(1) = 0. As x gets larger and larger, the argument and, therefore, the logarithm keep getting larger and larger too. So 0 is the lowest number in the range. All the other values for h(x) will be larger (i.e. positive). As x approaches infinity, so does h(x) (IOW there is no maximum value for h(x).). So the range is zero and all positive numbers.
|
|
|
