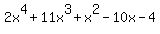
If it has any rational solutions the numerator must be
a factor of 4 and the denominator must be a factor of 2,
The only possible rational solutions are
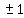 ,
, 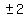 ,
, 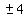 , or
, or  Trying the easiest one x = 1
So we divide by x - 1, either synthetically:
1|2 11 1 -10 -4
| 2 13 14 4
2 13 14 4 0
or by long division
2x³ + 13x² + 14x + 4
x - 1)2x4 + 11x³ + x² - 10x - 4
2x4 - 2x³
13x³ + x²
13x³ - 13x²
14x² - 10x
14x² - 14x
4x - 4
4x - 4
0
You have now factored the original polynomial as
(x - 1)(2x³ + 13x² + 14x + 4)
Next let's do the same with the cubic polynomial in
the second parenthesis:
If it has any rational solutions the numerator must be
a factor of 4 and the denominator must be a factor of 2,
We've already done that. The only possible rational solutions are
Trying the easiest one x = 1
So we divide by x - 1, either synthetically:
1|2 11 1 -10 -4
| 2 13 14 4
2 13 14 4 0
or by long division
2x³ + 13x² + 14x + 4
x - 1)2x4 + 11x³ + x² - 10x - 4
2x4 - 2x³
13x³ + x²
13x³ - 13x²
14x² - 10x
14x² - 14x
4x - 4
4x - 4
0
You have now factored the original polynomial as
(x - 1)(2x³ + 13x² + 14x + 4)
Next let's do the same with the cubic polynomial in
the second parenthesis:
If it has any rational solutions the numerator must be
a factor of 4 and the denominator must be a factor of 2,
We've already done that. The only possible rational solutions are
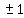 ,
, 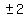 ,
, 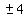 , or
, or  You could go to the trouble of trying all those. But sooner of
later you'd get around to trying to divide by
You could go to the trouble of trying all those. But sooner of
later you'd get around to trying to divide by  or
or  Divide by x + .5, either synthetically:
-.5|2 13 14 4
| -1 -6 -4
2 12 8 0
or by long division
2x² + 12x + 8
x + .5)2x³ + 13x² + 14x + 4
2x³ + x²
12x² + 14x
12x? + 6x
8x + 4
8x + 4
0
And you have now factored further as
(x - 1)(x + .5)(2x² + 12x + 8)
Now we can factor 2 out of the third parentheses:
(x - 1)(x + .5)2(x² + 6x + 4)
2(x - 1)(x + .5)(x² + 6x + 4)
The quadratic will not factor but we can find its roots
by using the quadratic formula:
Divide by x + .5, either synthetically:
-.5|2 13 14 4
| -1 -6 -4
2 12 8 0
or by long division
2x² + 12x + 8
x + .5)2x³ + 13x² + 14x + 4
2x³ + x²
12x² + 14x
12x? + 6x
8x + 4
8x + 4
0
And you have now factored further as
(x - 1)(x + .5)(2x² + 12x + 8)
Now we can factor 2 out of the third parentheses:
(x - 1)(x + .5)2(x² + 6x + 4)
2(x - 1)(x + .5)(x² + 6x + 4)
The quadratic will not factor but we can find its roots
by using the quadratic formula:


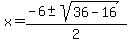





 So the 4 roots are
1,
So the 4 roots are
1,  ,
, 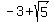 , and
, and 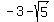 Edwin
Edwin