Find all sets of three consecutive odd integers whose sum is between 20 and 30.
The statement is not entirely clear as to whether the sum is to be
'inclusive' or 'excusive' of the two bounds. But it won't even matter,
because the sum of three odd integers must be odd, so it's definitely
exclusive.
What we require is this:
20 < n + (n+2) + (n+4) < 30
Remove the parentheses
20 < n + n + 2 + n + 4 < 30
Collect like terms
20 < 3n + 6 < 30
Add -6 to all three sides:
20 < 3n + 6 < 30
-6 -6 -6
-----------------
14 < 3n < 24
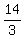< n < 8
< n < 8
The only odd integers that satify that are 5 and 7
So the only sets of three consecutive integers with a
sum in that domain are:
{5, 7, 9}, since 5 + 7 + 9 = 21
{7, 9, 11}, since 7 + 9 + 11 = 27
Edwin
