SOLUTION: If susan can pain a house in four hours, John can pain a house in six hours, and Peter can paint a house in ten hours. How long will it take if all of them painted the house togeth

Algebra ->  Average -> SOLUTION: If susan can pain a house in four hours, John can pain a house in six hours, and Peter can paint a house in ten hours. How long will it take if all of them painted the house togeth      Log On


   

Question 333860: If susan can pain a house in four hours, John can pain a house in six hours, and Peter can paint a house in ten hours. How long will it take if all of them painted the house together?
I tried averaging the numbers togther and then dividing it by three and sometimes its right and sometimes its wrong. Can you help?
Found 2 solutions by stanbon, jim_thompson5910:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
If susan can paint a house in four hours,
Susan rate = 1/4 job/hr.
-----------------------------
John can paint a house in six hours
John's rate = 1/6 job/hr
----------------------------------
and Peter can paint a house in ten hours
Peter's rate = 1/10 job/hr.
===============================
Together rate = 1/x job/hr.
===============================
How long will it take if all of them painted the house together?
Equation:
rate + rate + rate = together rate
1/4 + 1/6 + 1/10 = 1/x
-----
Multiply thru by 60 to get:
15x + 10x + 6x = 60
31x = 60
x = 60/31 = 1.9355 hrs (time required for them to do the job together)
========================
Cheers,
Stan H.
==========

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
"If susan can pain a house in four hours", then she can paint 1%2F4 of a house in 1 hour. So her rate is 1%2F4 houses per hour.


If "John can pain a house in six hours", then he can paint 1%2F6 of a house in 1 hour. So his rate is 1%2F6 houses per hour.


Finally, if "Peter can paint a house in ten hours", then he can paint 1%2F10 of a house in one hour, making his rate 1%2F10 houses per hour.


So the three rates are: 1%2F4, 1%2F6 and 1%2F10 houses per hour.


Add them up to get 1%2F4%2B1%2F6%2B1%2F10=15%2F60%2B10%2F60%2B6%2F60=31%2F60


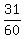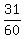So their combined rate is 31%2F60 houses per hour. In other words, together they can paint 31%2F60 of a house in one hour (which is close to 1/2 of a house).

Now multiply this rate by some unknown time 't' to get 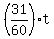%2831%2F60%29t and set that equal to 1 (since we want to paint one house) to get %2831%2F60%29t=1


Next, multiply both sides by 60 to get 31t=60 and then divide both sides by 31 to isolate t to get t=60%2F31=1.93548387


So it will take them about 1.935 hours, or close to 2 hours, if they work together.