SOLUTION: The Diagonals of Rhombus measure 16cm and 30cm.Find its perimeter

Here is the rhombus drawn twice, once with each diagonal.  The four
sides of a rhombus have equal measures. Let each side have length x.
Then the perimeter of the rhombus will be 4x.
  
The drawings below are to scale:



Looking at the lower triangular half of the left drawing we use the 
law of cosines on triangle ABC:









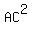
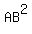
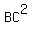
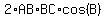
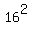
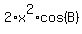
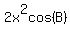Divide every term by 2



-------------------
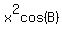Now we look at the left triangular half of the right drawing, and
we use the law of cosines again, this time on triangle ABD:










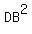
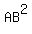
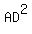
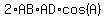
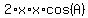
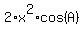
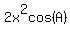Divide every term by 2



---------

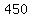
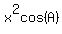Here are the two equations we have found above:




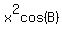
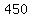
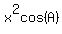A rhombus is a parallelogram, and the adjacent angles in a
parallelogram are supplementary.  Therefore the sum of the
measures of angles A and B is 180°.  Therefore

B = 180° - A

Therefore we use the identity:  ,

and get: 

cos(B) = cos(180°-A) = -cos(A) 

We substitute -cos(A) for cos(B) in the first equation and simplify:





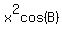
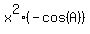
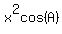Now we put that together with the other equation and we have this system:

 

When we add those two equations term-by term, the terms on the right cancel



and we get:



Divide both sides by 2



Taking positive square roots of both sides:





So the perimeter is 4x or 4(17) or 68.

Edwin