Question 332784: What are the foci of the ellipse x^2/16+y^2/49=1?
Answer by jrfrunner(365)   (Show Source): (Show Source):
You can put this solution on YOUR website! What are the foci of the ellipse  ? ?
==
 can be rewritten as can be rewritten as 
or in general
 for an ellipse with major axis along the x direction (note: for an ellipse with major axis along the x direction (note: 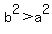 ) )
 for an ellipse with major axis along the y direction (note: for an ellipse with major axis along the y direction (note: 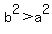 ) )
--

is an ellipse with the major axis along the y direction  and the minor axis along the x direction and the minor axis along the x direction
centered at (h,k)=(0,0)
----
In ellipses the focal length is 2*c, where c = 
so the foci for an ellipse with major axis along the y direction = (h,k-c), (h,k+c)
since h=0, k=0, c=5.745, the foci are at (0,-5.745) and (0,5.745)
|
|
|