Question 332248: Suppose that $2000 is invested at a rate of 6% per year compounded continuously. What is the balance after 1 yr? After 2 yrs?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Recall that the formula for continuous compounding interest is

where A is the return, P is the principal (amount invested), r is the interest rate (in decimal form) and t is the time in years.
Since "$2000 is invested at a rate of 6% per year compounded continuously", we know that  and and  (the decimal equivalent of 6%). (the decimal equivalent of 6%).
Now let's compute the return when  (ie find the balance after one year) (ie find the balance after one year)
 Start with the continuous compounding formula. Start with the continuous compounding formula.
 Plug in Plug in  , ,  , and , and  . .
 Multiply Multiply 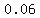 and and  to get to get 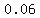 . .
 Raise 'e' (which is approximately 2.71828) to the power Raise 'e' (which is approximately 2.71828) to the power 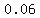 to get to get 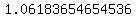 (this value is approximate). (this value is approximate).
 Multiply Multiply  and and 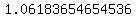 to get to get 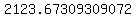 . .
 Round to the nearest hundredth (ie to the nearest penny). Round to the nearest hundredth (ie to the nearest penny).
So after 1 year, you'll have about $2,123.67
-----------------------------------------------------------------------------
Now let's compute the return when  (ie find the balance after two years) (ie find the balance after two years)
 Start with the continuous compounding formula. Start with the continuous compounding formula.
 Plug in Plug in  , ,  (the decimal equivalent of 6%), and (the decimal equivalent of 6%), and  . .
 Multiply Multiply 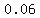 and and  to get to get  . .
 Raise 'e' (which is approximately 2.71828) to the power Raise 'e' (which is approximately 2.71828) to the power  to get to get 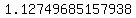 (this value is approximate). (this value is approximate).
 Multiply Multiply  and and 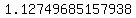 to get to get 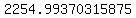 . .
 Round to the nearest hundredth (ie to the nearest penny). Round to the nearest hundredth (ie to the nearest penny).
So after two years, you'll have $2,254.99
|
|
|