Since the leading term (tho one with the largest
exponent is negative, we multiply every term by -1
so the leading term will be positive. So we
multiply through by -1. Thart changes all the signs:
Both the first term and the last term are perfect squares.
The first term 
is a perfect square, since it
can be written as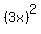 
. And the last term 
can
be written 
.
So the whole trinomial is a candidate for being a perfect square.
It may not be but we need to check to find out if it is actually
a perfect square. Here is the test:
Multiply the square roots of the first and last terms on the left.
Then double what you get. If you get the same thing as the middle
term, or the middle term with the opposite sign, then it is a perfect
square, and factors as
(Square root of first term, sign of muddle term, Square root of last term)2
The square roots are 3x and 4. Multiply them. Get 12x.
Then double that and get 24x. That is the same thing as the middle term
-24x, with the opposite sign, so it is a perfect square, and factors as
So there is only one solution, found by setting
Edwin
