SOLUTION: what are the x-intercepts and y-intercepts for the ellispe {{{x^2/9 + y^2/36 = 1}}}

The standard forms for an ellipse with center at the origin is:

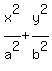
 for ellipses like this  where a > b

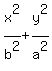
 for ellipses like this  where a < b



Since the larger number is under the expression in y the ellipse is 
of the form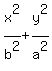  
and is like this  

 or , , or 

We start with a set of axes like this:




Let's draw a green vertical line beginning at the center, which is
(0,0) and going upward  units, which is one-half the
major axis.  This ends in the point (0,6) which is the upper
vertex, and which is one of the y-intercepts: 
 



Next we draw another vertical line beginning at the center
(0,0) and going downward  units, which is one-half the
major axis.  This ends in the point (0,-6) which is the lower
vertex, and which is the other y-intercept:  



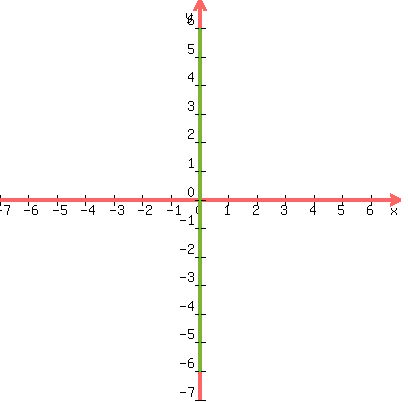That whole green line is the major axis, and it is 12 units long.
 

Let's draw a green horizontal line beginning at the center, which is
(0,0) and going left  units, which is one-half the
minor axis.  This ends in the point (-3,0) which is the left co-vertex,
and which is one of the x-intercepts: 
 



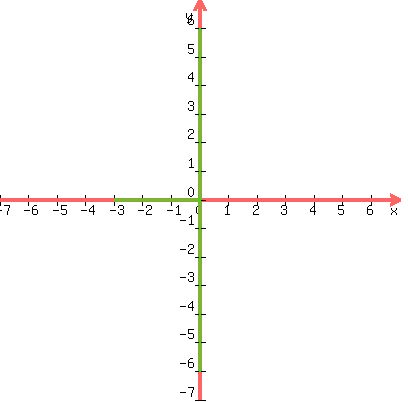Next we draw another green horizontal line beginning at the center
(0,0) and going right  units, which is one-half the
minor axis.  This ends in the point (3,0) which is the right
co-vertex, and which is the other x-intercept:  



That whole green line is the minor axis, and it is 6 units long.

Now we can sketch in the ellipse:



The x-intercepts are (-3,0) and (3,0)
The y-intercepts are the points (0,-6) and (0,6)

Edwin