SOLUTION: Please sketch this hyperbola and show me how you did it: x^2-y^2=1.

The equation

 is the equation of a hyperbola that opens
right and left with these properties:

1.  The center is at the origin (0,0).

2.  The vertices are the ends of the transverse axis (-a,0) and (a,0).

3.  The endpoints of the conjugate axis are (0,b) and (0,-b).

4.  The foci are the points (-c,0) and (c,0) where 

5.  The defining rectangle has the 4 corners 
    (-a,b), (-a,-b), (a,-b), and (a,b)

6.  The asymptotes are the extended diagonals of the defining rectangle
    and have equations 

Your equation is 



Write it as 



and we see that  and , so  and ,

so:

1.  The center is at the origin (0,0).

2.  The vertices are the ends of the transverse axis (-1,0) and (1,0).

3.  The endpoints of the conjugate axis are (0,1) and (0,-1).

4.  The foci are the points (-c,0) and (c,0) where 

    So we calculate 

    and the foci are (,0) and (,0) 


5.  The defining rectangle has the 4 corners 
    (-1,1), (-1,-1), (1,-1), and (1,1)

6.  The asymptotes are the extended diagonals of the defining rectangle
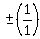
    and have equations , or
    

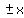So we draw the defining rectangle and its extended diagonals:


    
Now we sketch in the hyperbola:



Edwin