Question 329611: Hello, I am trying to figure out how to find the answer to a problem in an Appendix Application. It is to find out the weight of an object in Death Valley.
We are to use the formula  , ,  , , 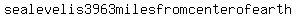 , finally Death Valley is 282 ft below sea level. , finally Death Valley is 282 ft below sea level.
In previous question I was to find "C" if an object weighed 100 lbs at sea level. C= 1,562,500,000 For this question,
I have figured out that sea level is 20,924,640 ft from center of earth, which makes Death Valley 20,924,358 ft.
From here my numbers are so big that they will not compute on my calculator, But if I try to covert the feet back to miles for Death Valley, I come up with the weight of 100 lbs, again. I do not think this would be right. Should I possibly be finding the perfect squares of some of these numbers and reducing them down somehow to get smaller numbers to find this wieght?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! The solution to your problem is as follos:
The equation you have is:
w = c * r^-2
This is the same as w = c / r^2
c is a constant.
r is the distance from the center of the earth.
r is given in miles, so you would need to either translate your elevation to miles or you would need to translate the distance to the center of the earth to feet.
I chose to translate the distance to the center of the earth to feet.
At sea level the object is 3963 miles from the center of the earth.
Multiply that by 5280 and the object is 20924640 feet from the center of the earth.
You are given that the weight of the object is 100 pounds at sea level.
You are also given that the equation w = c / r^2 is true at sea level.
You can use the weight of the object at sea level to calculate the value of c.
You get 100 = c / r^2 which becomes 100 = c / 20924640^2
Multiply both sides of this equation by 20924640^2 to get c = 100 * 20924640^2
That's the value of c and it will not change because it is a constant.
r will change, however, because it is the distance from the center of the earth.
To test the equation to see if it is true at sea level, then just substitute
what you know and solve.
The equation at sea level is:
100 = c / r^2
Since c = 100 * 20924640^2 and r = 20924640, then you get:
100 = 100 * 20924640^2 / 20924640^2 which becomes 100 = 100 which is true.
You have confirmed the equation is true at sea level, so you can be comfortable that you calculated the value of c correctly
Your first question is how much does an object weigh that is 282 feet below sea level.
The equation is w = c / r^2
c is a constant of 100 * 20924640^2
r is now 20924640 - 282 = 20924358
Your equation becomes:
w = 100 * 20924640^2 / 20924358^2 = 100.0026954 pounds.
You can also keep everything as miles and you will get the same answer.
Your equation is w = c*r^-2 which is the same as c/r^2.
r is the distance from the center of the earth.
At sea level, this distance is 3963 miles.
This is equivalent to 5280 * 3963 = 202924640 feet which is what you got before.
282 feet below sea level would therefore be 20294640 - 282 = 20924358 feet.
Divide that by 5280 and you get 3962.946591 miles.
You find c at sea level by using the formula 100 = c/r^2 which becomes 100 = c/3963^2.
Multiply both sides of this equation by 3963^2 to get c = 100 * 3963^2.
that's your constant.
To find w 282 feet below sea level, the formula becomes:
w = c / (3962.946591)^2
Since c = 100 * 3963^2, this formula becomes:
w = (100 * 3963^2) / (3962.946591)^2 which becomes:
w = 100.0026954.
You get the same answer whether or not you used feet as a measure or miles as a measure.
If your calculator is a scientific calculator, it should be able to handle these large numbers internally.
You can then store the intermediate results in memory and recall the number when needed.
My calculator is a TI-30XA which is a pretty cheap scientific calculator (costs around $10 to $15 Dollars.
3963 squared shows up as 15705369.
(3963 * 5280) squared shows up as 4378405591 * 10^14.
To calculate w = 100 * 20924640^2 / 20924358^2, I do the following:
Enter 100
Multiply it by 20924640^2 to get 4.378405591 * 10^16.
Divide that by 20924358^2 to get 100.0026954.
If you don't have a scientific calculator, then use an online scientific calculator.
One such calculator would be found here:
http://web2.0calc.com/
You enter your formula in the white box.
When you hit return, you get your answer in the white box and the formula you entered is shown above.
I entered:
(100 * (3963*5280)^2) / (3963*5280-282)^2
and I got:
100.00269544136335
I also entered the same formula in my TI-30XA calculator and I got:
100.0026954.
My calculator is not capable of displaying the same number of digits as this online calculator, but the answer is still the same to the degree of precision that my calculator can display.
|
|
|