|
Question 329448: Can you show me how to get the equation of a parabola with a focus (17,9) and a directrix x=12?
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can you show me how to get the equation of
a parabola with a focus (17,9) and a directrix x=12.
---------------
Draw the picture of the line and and the point.
---
The vertex is half way between at (19.5, 9)
---
p is the distance from the vertex to the focus = 2.5
-------------
Form: (y-k)^2 = 4p(x-h)
---
(y-9)^2 = 8(x-(39/2))
===========================
Cheers,
Stan H.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can you show me how to get the equation of a parabola with a focus (17,9) and a directrix x=12?
The other tutor got the vertex wrong.
Let's draw the directrix line and the vertex:
 The vertex is halfway between the focus and the directrix.
We draw a green line from the focus to the directrix
The vertex is halfway between the focus and the directrix.
We draw a green line from the focus to the directrix
 That green line is 5 units long, so the midpoint of the green line,
which is the vertex, is
That green line is 5 units long, so the midpoint of the green line,
which is the vertex, is  units from the directrix and the
focus. So the coordinates of the vertex is ( units from the directrix and the
focus. So the coordinates of the vertex is (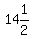 ,9) or
( ,9) or
(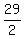 ,9) ,9)
 To sketch in the parabola we construct two squares, one on each side of
the green line from vertex to focus:
To sketch in the parabola we construct two squares, one on each side of
the green line from vertex to focus:
 Now we can sketch in the parabola with the vertex and which passes
through the corners of those two squares:
Now we can sketch in the parabola with the vertex and which passes
through the corners of those two squares:
 The equation of the parabola which opens right or left and has vertex (h,k)
is given by:
The equation of the parabola which opens right or left and has vertex (h,k)
is given by:
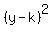  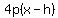 where p is the
where p is the  or or  unit distance between the
directrix and the vertex, and also the same distance from the vertex
to the focus. p is taken positive if the parabola opens right, and
negative if the parabola opens left.
This parabola opens right so unit distance between the
directrix and the vertex, and also the same distance from the vertex
to the focus. p is taken positive if the parabola opens right, and
negative if the parabola opens left.
This parabola opens right so  , and with the vertex
(h,k) = ( , and with the vertex
(h,k) = (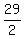 ,9) ,9)
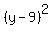  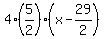
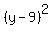  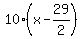 That's the equation of the parabola in standard form.
Edwin
That's the equation of the parabola in standard form.
Edwin
|
|
|
| |