Question 329421: A plane travels at 120 mph in still air. It is headed due south in a wind of 30 mph from the northeast. What is the resultant velocity of the plane? Find the magnitude and the drift angle. The drift angle is the angle between the intended line of flight and the true line of flight.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's define a coordinate system where East is positive  , North is positive , North is positive  . .
Without wind, the plane would travel with velocity ( , ,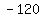 ). ).
From the northeast to the southwest direction is  degrees if the positive x axis is degrees if the positive x axis is  degrees. degrees.
The wind velocity is ( , ,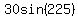 )=( )=(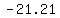 , ,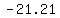 ) )
So the resultant velocity is (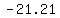 , ,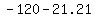 )=( )=(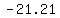 , ,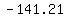 ). ).
The magnitude of the resultant is
 mph mph
The tangent of the angle of the resultant is,

so then,
 degrees degrees
Since the plane should be traveling at due South ( degrees), the drift angle is degrees), the drift angle is
 degrees West of South degrees West of South
|
|
|