SOLUTION: A drug is known to be 80% effective in curing a certain disease. If four people with the disease are to be given the drug, the probability that more than two will be cured is:

Algebra ->  Probability-and-statistics -> SOLUTION: A drug is known to be 80% effective in curing a certain disease. If four people with the disease are to be given the drug, the probability that more than two will be cured is:      Log On


   

Question 328703: A drug is known to be 80% effective in curing a certain disease. If four people with the disease are to be given the drug, the probability that more than two will be cured is:
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!
A drug is known to be 80% effective in curing a certain disease. If four people with the disease are to be given the drug, the probability that more than two will be cured is:

The binomial probability of exactly x successes in n independent trials, when
the probability of exactly one success in one trial is p, is given by:

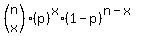%28matrix%282%2C1%2Cn%2Cx%29%29%28p%29%5Ex%2A%281-p%29%5E%28n-x%29

Here there are n trials so n = 4.  The probability of one success (cure) in 1
trial is .8, so p=.8

"More than two" means "three or four", and "or" means to add, so

the probability of 3 or 4 being cured is

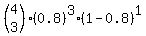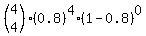
%28matrix%282%2C1%2C4%2C3%29%29%280.8%29%5E3%281-0.8%29%5E1%22%22%2B%22%22%28matrix%282%2C1%2C4%2C4%29%29%280.8%29%5E4%281-0.8%29%5E0

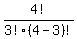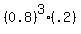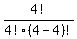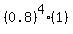
4%21%2F3%21%284-3%29%21%280.8%29%5E3%28.2%29%22%22%2B%22%224%21%2F4%21%284-4%29%21%280.8%29%5E4%281%29

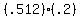4%21%2F3%211%21%28.512%29%28.2%29%22%22%2B%22%224%21%2F4%210%21.4096

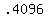
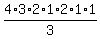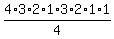4%2A3%2A2%2A1%2F3%2A2%2A1%2A1.1024%22%22%2B%22%224%2A3%2A2%2A1%2F4%2A3%2A2%2A1%2A1.4096

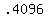
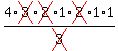4%2Across%283%29%2Across%282%29%2A1%2Fcross%283%29%2Across%282%29%2A1%2A1.1024%22%22%2B%22%22.4096

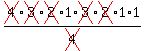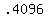
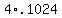4%2A.1024%22%22%2B%22%22.4096

.4086%22%22%2B%22%22.4086

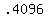
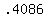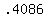.8192

You can also find that in the binomial table in your book
with n = 4 and p = .8

Or if you have a TI-83 or TI-84 calculator

On the calculator you have to consider the complement event as
1 - probability that 2 or fewer will be cured:
 
Press ON
Press CLEAR

Type 1-

Press 2ND
Press VARS
Press ALPHA
Press APPS

You should see this -->    1-binomcdf(   
followed by a blinking cursor.
After the parenthesis type this -->  4,.8,2)

You should see this -->    1-binomcdf(4,.8,
                           2)

Press ENTER

You should see the answer .8192

Edwin