SOLUTION: If ABCD is a parallelogram with A(2,1,4), B(1,4,3) and C(1,0,2), find: (a) the area of the parallelogram (b) the coordinate of D

Algebra ->  Vectors -> SOLUTION: If ABCD is a parallelogram with A(2,1,4), B(1,4,3) and C(1,0,2), find: (a) the area of the parallelogram (b) the coordinate of D      Log On


   

Question 328183: If ABCD is a parallelogram with A(2,1,4), B(1,4,3) and C(1,0,2), find:
(a) the area of the parallelogram
(b) the coordinate of D
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Since A is the point (2,1,4) and B is the point (1,4,3), the vector from A to B
is 

< 1-2, 4-1, 3-4 > or < -1, 3, -1 >

Since B is the point (1,4,3) and C is the point (1,0,2), the vector from B to C
is 

< 1-1, 0-4, 2-3 > or < 0, -4, -1 >

Since those vectors are adjacent sides of a parallelogram, the
area of the parallelogram is the magnitude of their cross
product. So we find their cross product:

 = (-3-4)i - (1-0)j + (4-0)k = -7i - j +4k

And the magnitude of their cross product is 

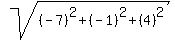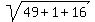sqrt%28%28-7%29%5E2%2B%28-1%29%5E2%2B%284%29%5E2%29%22%22=%22%22sqrt%2849%2B1%2B16%29%22%22=%22%22sqrt%2866%29
      
(b)

Let D be the point (x1, y1, z1).  Since A is the point (2,1,4),
then the vector from A to D is < x1-2, y1-1, z1-4 >

Since C is the point (1,0,2) and B is the point (1,4,3),

the vector from B to C is < 1-1, 0-4, 2-3 > or < 0, -4, -1 >

Since opposite sides of a parallelogram are equal and parallel,

they must be the same vector.  Therefore we set the corresponding

components  of the vector from A to D,  < x1-2, y1-1, z1-4 > and the vector from B to C < 0,-4,-1 >

equal:

x1-2 = 0, y1-1 = -4, z1-4 = -1,

so

x1=2, y1=-3, z1=3

and the point D is (x1, y1, z1) = (2,-3,3)

Edwin