Question 327541: A vector is described. Express the vector in terms of i and j. If exact values are not possible, round components to the nearest tenth.
A plane with an airspeed of 450 mph is flying in the direction N35W.
I have gotten an answer but am not sure if I have done it right. I need some help on this to make sure. Are you to use bearings?
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! A vector is described. Express the vector in terms of i and j. If exact values are not possible, round components to the nearest tenth.
A plane with an airspeed of 450 mph is flying in the direction N35W.
I have gotten an answer but am not sure if I have done it right. I need some help on this to make sure. Are you to use bearings?
North is the positive y-axis
South is the negative y-axis
East is the positive x-axis
West is the negative x-axis
This is the vector. Its direction is determined by starting from
north, the positive y-axis, and swinging a vector toward the west,
which is counter-clockwise, by 35°.
 To express this vector in terms of horizontal and vertical
component vectors, we draw horizontal and vertical lines from the
tip of that vector to the x and y axes:
To express this vector in terms of horizontal and vertical
component vectors, we draw horizontal and vertical lines from the
tip of that vector to the x and y axes:
 Then these two green vectors are the x-component
and y-component of the red vector:
Then these two green vectors are the x-component
and y-component of the red vector:
 The actual angle is this vector measured from the
postive x axis, indicated by this blue arc, which is
90°+35° or 125°
The actual angle is this vector measured from the
postive x axis, indicated by this blue arc, which is
90°+35° or 125°
 The magnitude of the green horizontal vector is
The magnitude of the green horizontal vector is  Therefore it is the vector
Therefore it is the vector  i
The magnitude of the green vertical vector is i
The magnitude of the green vertical vector is  Therefore it is the vector
Therefore it is the vector  j
So to write the red vector in terms of the horizontal unit vector
i and the vertival unit vector j, we have j
So to write the red vector in terms of the horizontal unit vector
i and the vertival unit vector j, we have
 i + i +  j
There is no way to get the exact values, so we punch those into a
calculator and get: j
There is no way to get the exact values, so we punch those into a
calculator and get:
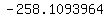 i + i + 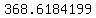 j
Or rounded to tenths: j
Or rounded to tenths:
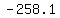 i + i + 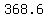 j
Edwin j
Edwin
|
|
|