Question 327037: Twelve $5-bills, eight $10-bills, and five $20-bills are put into a bag and shaken up. You get to reach in and pull out two of the bills without looking. What is the probability you get a total of at least $20?
a 46% b 54% c 66 2/3% d 33 1/3% e 60%
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! 12 $5, 8 $10, 5 $20=25 bills total
.
.
.
Remember for the second probability, the total number of bills is reduced by 1.
1.
2.
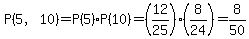
3.
4.
5.
6.
7.
8.
9.
.
.
.
If you add all of these probabilities together, you will get  , since these outcomes represent all of the possible outcomes.
.
.
.
Now find, the ones that sum to at least $20 and add up their probabilities.
3,5,6,7,8,9 all sum to at least $20. Add up all of their probabilities or you could add 1,2, and 4 probabilities and subtract from 1.
.
.
.
P(>=$20)= or 46%
|
|
|
