Question 326968: I am still having trouble on this can some one please make it a little clearer for me on how to get the answer to this. i am having trouble showing the work on this.
1. Construct a scatter plot using excel for the given data. Determine whether there is a positive linear correlation, negative linear correlation, or no linear correlation. Complete the table and find the correlation coefficient r. (References: example 1 - 4 pages 498 - 500; end of section exercises 15 - 22 pages 508 - 509)
The data below are the number of absences and the final grades of 9 randomly selected students from a statistics class.
Absences, x 4 7 10 8 13 6 19 12 9
Final grade, y 99 87 81 83 72 93 56 77 83
a: Scatter plot (3.5 points)
b: Type of correlation (positive linear correlation, negative linear correlation, or no linear correlation) (2.5 points)
c: Complete the table and find the correlation coefficient r.
(6 points)
x y xy x2 y2
4 99
7 87
10 81
8 83
13 72
6 93
19 56
12 77
9 83
Use the last row of the table to show the column totals.
n = 9
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! a) Enter the data into two columns in an Excel spreadsheet.
Highlight the columns and hit the Chart Wizard button.
Choose scatterplot.
b) Looking at the scatterplot, you can make a good guess about the correlation.
.
.
.
To get an actual  value do the following.
Once you finish the chart, right click on a data point.
Choose "Add trendline".
Under Type tab, choose Linear.
Go to the Options tab.
Click "Display equation on Chart" and "Display R-sqaured value on Chart".
Read the 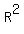 value off of the chart.
c) X values in column 1, rows 1-9
Y values in column 2, rows 1-9
Find the average of the x values, xave=9.78.
Find the average of the y values, yave=81.22.
Generate a new column (column 3) equal to (x-9.78), in EXCEL the formula would be "=A1-9.78" for column 3, row 1, cell. Copy this formula down the column.
Generate a new column (column 4) equal to (y-81.22), in EXCEL the formula would be "=B1-81.22" for column 4, row 1, cell. Copy this formula down the column..
Generate a new column (column 5) equal to (x-9.78)^2, in EXCEL the formula would be "=C1^2" for column 5, row 1, cell. Copy this formula down the column.
Generate a new column (column 6) equal to (y-81.22)^2, in EXCEL the formula would be "=D1^2." for column 6, row 1, cell. Copy this formula down the column.
Generate a new column (column 7) equal to (x-9.78)(y-81.22), in EXCEL the formula would be "=C1*D1." for column 7, row 1, cell. Copy this formula down the column.
Sum the values for column 5 (SSXX), column 6 (SSYY), and column 7 (SSXY).
Find the value of SSXY/SSXX, that is b the slope of the regression line.
Find the value of SSXY/SSYY, call that b'.
By definition, r^2=b*b'
So then to find r, take the square root.
It's actually easier than it looks.
As a check, you should get the
SSXX=159.56
SSYY=1233.56
If not, there's a mistake somewhere.
.
.
.
For a more technical explanation, check out http://mathworld.wolfram.com/LeastSquaresFitting.html
|
|
|
