Question 326194: Sove using factoring and principle of zero products. Must show all work. (please explain how you did this so I can try to understand) Thank you in advance:
2x^2+x=42+9x
Found 2 solutions by scott8148, Edwin McCravy:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! subtracting 42+9x ___ 2x^2 - 8x - 42 = 0
the factors of 2x^2 are 2x and x
the factors of -42 are (±1, ±42), (±2, ±21), (±3, ±14), (±6, ±7)
you need to "combine" the 2x and x with one of the other pairs of factors to end up with -8x
___ the "combining" is summing the products of the pairs by FOILing
2x times 3 is 6x ___ x times -14 is -14x ___ this gives you the -8x
so the factors are ___ (2x - 14) and (x + 3) ___ (2x - 14)(x + 3) = 0
the zero principle means that any (or all) of the quantities, whose product is zero, must be zero
2x - 14 = 0 ___ 2x = 14 ___ x = 7
x + 3 = 0 ___ x = -3
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! 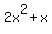  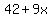
The other tutor's solution is correct; however there is one step
he did not do, which would have made the factoring easier.
Get a zero on the right by adding 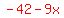 to both sides to both sides
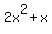 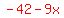  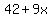 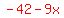 Combine like terms and simplify:
Combine like terms and simplify:
  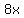     Since all the numbers are even we can divide every term by
Since all the numbers are even we can divide every term by 
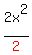  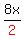  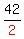  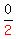 [That is the step which the other tutor did not do, which makes it easier
to factor.]
Simplify:
[That is the step which the other tutor did not do, which makes it easier
to factor.]
Simplify:
  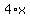  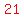   We must factor that.
I did some coloring so I can refer to the parts:
List all the ways to factor the red number 21 using two factors,
(list the larger factor first):
We must factor that.
I did some coloring so I can refer to the parts:
List all the ways to factor the red number 21 using two factors,
(list the larger factor first):
  
  
  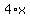     Notice that the red sign (the one just before the 21 is
Notice that the red sign (the one just before the 21 is  Put that sign between those numbers above instead of the multiplication
sign, and give the answer:
Put that sign between those numbers above instead of the multiplication
sign, and give the answer:
    
    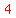 Notice that the
Notice that the 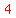 is the same as the middle coefficient
ignoring the sign: is the same as the middle coefficient
ignoring the sign:
  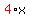     Therefore write this:
Therefore write this:
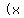   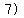 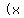   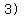   Finally we put the signs in. 7 is the larger factor, and the red
sign (the sign before the
Finally we put the signs in. 7 is the larger factor, and the red
sign (the sign before the 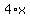 is is  in this: in this:
  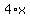     So we place that sign before the 7
So we place that sign before the 7
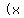  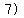 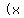   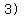   Next we place whichever sign before the 3 which will cause the product
to come out to be
Next we place whichever sign before the 3 which will cause the product
to come out to be 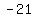 , the last term of , the last term of   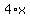     That sign would have to be
That sign would have to be  , so we have
now completely factored the left side: , so we have
now completely factored the left side:
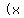  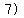 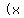  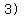   Next we use the zero-factor principle.
Each of the factors
Next we use the zero-factor principle.
Each of the factors 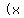  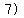 and and 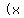 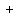 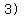 represents some number.
Since their product must equal to 0,
it is obvious that one of them is equal to 0. But which one?
We cannot tell, so it would be correct if represents some number.
Since their product must equal to 0,
it is obvious that one of them is equal to 0. But which one?
We cannot tell, so it would be correct if 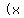  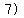 were
0 and were
0 and 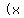  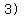 something else. OR, it would also
be correct if something else. OR, it would also
be correct if 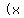  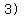 were 0 and were 0 and 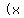  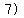 were something else.
That's why there are two solutions to a quadratic equation. So we
have to consider both possibilities: were something else.
That's why there are two solutions to a quadratic equation. So we
have to consider both possibilities:
     OR OR      Solvving those we have two possibilities for solutions:
Solvving those we have two possibilities for solutions:
   OR OR    Edwin
Edwin
|
|
|