SOLUTION: For how many values of n where n≤100 is 1/n represented by a terminating decimal?

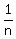 will be a terminating decimal if and only if 
its only prime factors are 2 and 5 (the prime factors of 10)

all the powers of 2 under 100 are

2, 4, 8, 16, 32, 64

That's the first set of numbers

all the powers of 5 under 100 are

5, 25

1 over any of those will be a terminating decimal.

But that's not all,

1 over any product of those will also be a terminating decimal.

Now we get all the products of one of the first set
times one of the numbers in the second set.

the only products of those are

2*5=10, 4*5=20, 8*5=40, 16*5=80, (32x5 is over 100 so we stop)

2*25=50, 4*25=100, (8*25 is over 100 so we stop)

So the only cases are

 1. 
 2. 
 3. 
 4. 
 5. 
 6. 
 7. 
 8.  
 9. 
10. 
11. 
12. 
13. 
14. 

So there are 14.

Edwin