Question 325483: Find the center, foci, vertices, length of major axis, and length of minor axis of the ellipse 25(x-2)^2 + 4(y+5)^2 = 100. Sketch the graph of the ellipse. Thanks in advance... (^2 means squared)
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The standard forms for ellipses are
   for ellipses like this for ellipses like this  where a > b where a > b
   for ellipses like this for ellipses like this  where a < b where a < b
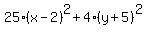   To get 1 on the right, divide through by
To get 1 on the right, divide through by 
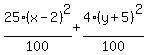   Simplify:
Simplify:
   Since the larger number is under the expression in y the ellipse is
of the form
Since the larger number is under the expression in y the ellipse is
of the form    and is like this
and is like this 
 , ,  , ,  or or  , ,  , or , or  center = (h,k) = (2,-5)
So let's begin by plotting the center (2,-5)
center = (h,k) = (2,-5)
So let's begin by plotting the center (2,-5)
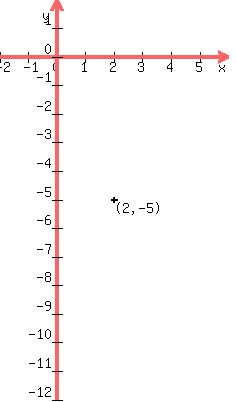 Next we draw a vertical line beginning at the center
(2,-5) and going upward
Next we draw a vertical line beginning at the center
(2,-5) and going upward  units, which is one-half the
major axis. This ends in the point (2,0) which is the upper
vertex. units, which is one-half the
major axis. This ends in the point (2,0) which is the upper
vertex.
 Next we draw a vertical line beginning at the center
(2,-5) and going downward
Next we draw a vertical line beginning at the center
(2,-5) and going downward  units, which is one-half the
major axis. This ends in the point (2,-10) which is the lower
vertex. That green line is the major axis, and it is 10 units long. units, which is one-half the
major axis. This ends in the point (2,-10) which is the lower
vertex. That green line is the major axis, and it is 10 units long.
 Next we draw a horizontal line beginning at the center
(2,-5) and going to the right
Next we draw a horizontal line beginning at the center
(2,-5) and going to the right  units, which is one-half the
minor axis. This ends in the point (4,-5) which is the right co-vertex. units, which is one-half the
minor axis. This ends in the point (4,-5) which is the right co-vertex.
 Next we draw a horizontal line beginning at the center
(2,-5) and going to the leftt
Next we draw a horizontal line beginning at the center
(2,-5) and going to the leftt  units, which is one-half the
minor axis. This ends in the point (0,-5) which is the left co-vertex.
The horizontal green line is is the minor axis, and it is 4 units long. units, which is one-half the
minor axis. This ends in the point (0,-5) which is the left co-vertex.
The horizontal green line is is the minor axis, and it is 4 units long.
 Now we can sketch in the ellipse:
Now we can sketch in the ellipse:
 Finally we find the foci. They are the two points on the major axis
w2hich are c units from the center, where c is calculated by
Finally we find the foci. They are the two points on the major axis
w2hich are c units from the center, where c is calculated by




 So we add
So we add  to the y-coordinate of the center
to find the upper focus, which is the point
(2, to the y-coordinate of the center
to find the upper focus, which is the point
(2, ), which is about (2,9.6),
marked in red below. ), which is about (2,9.6),
marked in red below.
 And we subtract
And we subtract  from the y-coordinate of the center
to find the lower focus, which is the point
(2, from the y-coordinate of the center
to find the lower focus, which is the point
(2,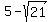 ), which is about (2,0.4),
also marked in red below. ), which is about (2,0.4),
also marked in red below.
 Edwin
Edwin
|
|
|