|
Question 324004: Farmer John stores grain in a large silo located at the edge of his farm.. The cylinder-shaped silo has one flat, rectanular face that rests against the side of his barn. The height of the silo is 30 feet and the face resting against the barn is 10 feet wide. If the barn is approximately 5 feet from the center of silo, determine the capacity of Farmer John's silo in cubic feet of grain.
Isn't the capacity the same as volume, so I need to use the formula lxwxh. Does the silo means this is an inscribed square. Do I need to find the area of the rectangle and the area of the square. I really do not understand how I am suppose to set this up.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Farmer John stores grain in a silo. The silo is cylinder-shaped.
It has one flat rectangular face that rests against the side of the barn.
The height of the silo is 30 feet and the face resting against the barn is 10 feet wide.
If the barn is approximately 5 feet from the center of the silo, determine the
capacity of the silo in cubic feet of grain.
:
The capacity is the same as the volume here.
This is the way I understand the problem
Draw the base of the silo, a circle with a 10' chord, 5' from the center.
Draw the triangle formed by these values and the center.
:
Find the radius of the silo using the flat side as a chord (10')
which forms two right triangles with legs of 5', hypotenuse is the radius.
r = 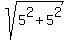
r = 7.07 ft
:
Find the area of the circular base ignoring the flat side for now
A = 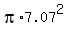
A = 157 sq/ft
:
A right triangle is formed by the 10' side and the two radii. the angle at the
center forms an arc that is 1/4 of the base. Remove this, that leaves the area of 3/4 of the base
.75(157) = 118 sq/ft
:
Add the area of the right triangle to this, because this has to be included
A = 118 + (.5*7.07*7.07)
A = 118 + 25
A = 143 sq/ft, the area of the base
:
Find vol of the 30 ft silo
V = 143 * 30
V = 4,290 cu/ft
:
:
Did this make sense to you? Let me know in the comment section.
|
|
|
| |