Question 323691: The amount of soda a dispensing machine pours into a 12 ounce can of soda follows a normal distribution with a mean of 12.03 ounces and a std deviation of 0.2 ounces. what portion of the soda can contains more than the 12 ounces advertised
Found 2 solutions by Fombitz, Edwin McCravy:
Answer by Fombitz(32388)   (Show Source):
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website! The amount of soda a dispensing machine pours into a 12 ounce can of soda follows a normal distribution with a mean of 12.03 ounces and a std deviation of 0.2 ounces. what portion of the soda can contains more than the 12 ounces advertised
Draw a normal curve on the x-axis marking the middle point
as the mean 12.03. Then mark off units right and left by adding the
standard deviation 0.2 to the mean to mark points to the right and
subtracting 0.2 from the mean to get points on the left side.
We'll draw a green "cut-off" line at 12.00, that's just a little bit
left of the middle 12.03:
We want the area to the right of the green line, for that area will be equal
to the desired portion (the portion of the cans which contain more than
12 ounces:
The area to the right of the green line is in two parts. The
left part of that area is the tiny strip between the green line
and the middle, which is marked with a red A.
The right part is the area under the entire right side
of the curve, marked with a red B=0.5.
and that area we already know is 0.5.
To find the area of the little strip marked A we must convert from a graph
with an x-axis to a graph with the corresponding z-axis with z-values
(or z-scores) instead of actual values in ounces.
The z-score of the mean is 0, so we put z=0 on the z-axis to correspond
to the mean x=12.03. We put z=1 to correspond to the value which is 1
standard deviation above the mean, that is z=1 on the z-axis corresponds
to 12.23 on the x-axis, and z=2 corresponds to 12.43 for that is 2
standard deviations above the mean. Similarly on the left side, the
two values on the z-axis with are 1 and 2 standard deviations below the
mean as z=-1 and z=-2.
But we must calculate the z-score that corresponds to x=12:
     
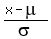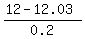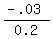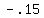
To find the area of the little strip on the left marked "A", we
look in the z-table for 0.1 on the far left and go across the top
to the column headed .05 and we read 0.0596. This is the area of
the little strip marked A. We add that to the whole right side
area which has value 0.5, and therefore the total area to the
right of the green line is 0.5000 + 0.0596 = 0.5596.
That is the answer, but you may want to express it as 55.96% of
the cans will contain more than 12 ounces.
-----------------------
You can do that very quickly if you have a TI-83 or TI-84 calculator.
You do not have to calculate any z-scores:
Press ON
Press CLEAR
Press 2ND
Press VARS
Press 2
You see ---> normalcdf(
followed by a blinking cursor
type in this ---> 12,99999999,12.03,0.2)
You now should see ---> normalcdf(12,999
99999,12.03,0,0.2)
Press ENTER
Read ---> .5596177121.
Round that to .5596. So 55.96% of the cans contain
more than 12 ounces.
Edwin
|
|
|
