|
Question 32369: I have a parabola that has a vertex at (0,16) and crosses the x-axis at (0,-16) and (0, 16) What is the equation?
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you have such a parabola, I would immediately call "Ripley's Believe it or not"
It is not possible to graph a parabola whose vertx is at (0, 16) with x-intercepts at (0, -16) and (0, 16).
I expect that you have inadvertently interchanged the x- and y-coordinates of your x-intercept points.
I think that the x-intercepts really should be: (-16, 0) and (16, 0), so we'll proceed on this assumption.
Since you are given the location of the vertex, let's use the "vertex" form of the equation for a parabola: for which we know that the vertex of the parabola is located at (h, k), so h = 0 and k = 16, thus wre can write: for which we know that the vertex of the parabola is located at (h, k), so h = 0 and k = 16, thus wre can write:
 But now we need to find the value of a. But now we need to find the value of a.
Now, the value of the y-coordinate of the vertex is positive and the parabola crosses the x-axis, it must therefore open downward and sign of a must be negative.
 so let's find the value of a by substituting one of the x-intercept point into this equation. Lets use (16, 0) so let's find the value of a by substituting one of the x-intercept point into this equation. Lets use (16, 0)
 solve for a. Subtract 16 from both sides. solve for a. Subtract 16 from both sides.
 Divide both sides by Divide both sides by 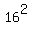
 Simplify. Simplify.
 Now you can write the equation of the parabola. Now you can write the equation of the parabola.

Here's the graph:

|
|
|
| |