SOLUTION: give exact and approximate solutions to three decimal places x^2+14x+49=25

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: give exact and approximate solutions to three decimal places x^2+14x+49=25      Log On


   

Question 323632: give exact and approximate solutions to three decimal places
x^2+14x+49=25
Answer by JBarnum(2146) About Me  (Show Source):
You can put this solution on YOUR website!
x^2+14x+49=25
x^2+14x+24=0
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B14x%2B24+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2814%29%5E2-4%2A1%2A24=100.

Discriminant d=100 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-14%2B-sqrt%28+100+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%2814%29%2Bsqrt%28+100+%29%29%2F2%5C1+=+-2
x%5B2%5D+=+%28-%2814%29-sqrt%28+100+%29%29%2F2%5C1+=+-12

Quadratic expression 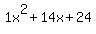1x%5E2%2B14x%2B24 can be factored:
1x%5E2%2B14x%2B24+=+1%28x--2%29%2A%28x--12%29
Again, the answer is: -2, -12. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B14%2Ax%2B24+%29