Question 323527: Hello, Can someone please help me with this problem I am stuck and not sure how get the answers.
In a survey of 163 dancers, 95 knew the Salsa, 129 knew the Merengue, and 89 knew the Cha Cha. Of these, 80 knew the Merengue and Salsa dances, 52 knew the Salsa and Cha Cha, and 75 knew the Merengue and Cha Cha. Fifty dancers knew all three dances.
Create a Venn diagram to reflect the above data, label your diagram clearly Use your diagram to answer the following questions here.
(a) How many knew only the Salsa?
(b) How many knew only the Cha Cha?
c) How many knew exactly two of the three dances?
(d) How many knew the Merengue and Salsa, but not the Cha Cha?
(e) How many knew none of these dances?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! It was a chore, but here's the breakdown.
Your Venn Diagram looks like this:
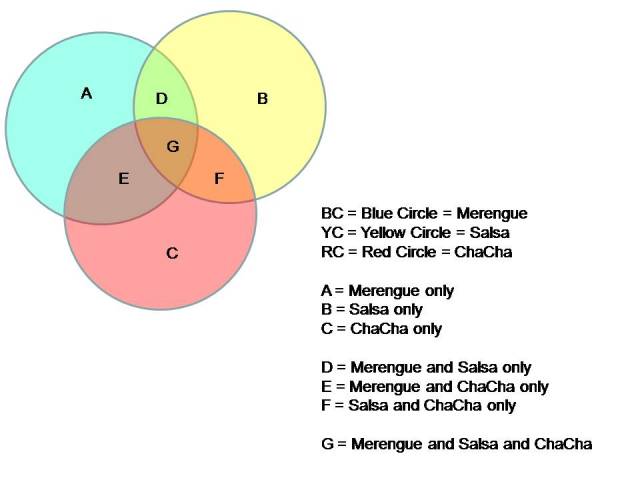
BC = Blue Circle = Merengue
YC = Yellow Circle = Salsa
RC = Red Circle = ChaCha
From the diagram you can see that:
BC = Merengue = A + D + E + G
YC = Salsa = B + D + F + G
RC = ChaCha = C + E + F + G
Your answer is:
A = 24 = Merengue only.
B = 13 = Salsa only.
C = 12 = ChaCha only.
D = 30 = Merengue and Salsa only.
E = 25 = Merengue + ChaCha only.
F = 2 = Salsa and ChaCha only.
G = 50 = Merengue and Salsa and ChaCha.
N = 7 = Dancers that do not know any of [Merengue, Salsa, ChaCha]
N is not shown on the Venn Diagram because it is outside of all the circles.
Total dancers = sum of the above = 163 as given.
You are given that:
Dancers that know Merengue = 129
That would be equal to A + D + E + G which would be equal to 24 + 30 + 25 + 50.
Dancers that know Salsa = 95
That would be equal to B + E + F + G which would be equal to 13 + 30 + 2 + 50.
Dancers that know ChaCha = 89
That would be equal to C + E + F + G which would be e4qual to 12 + 25 + 2 + 50.
To figure out the numbers, you work from the center out.
You are given that:
BC = Merengue = 129 = A + D + E + G
YC = Salsa = 95 = B + D + F + G
RC = ChaCha = 89 = C + E + F + G
You are also given that:
D + G = Merengue + Salsa = 80 (Intersection of Blue Circle and Yellow Circle).
E + G = Merengue + ChaCha = 75 (Intersection of Blue Circle and Red Circle).
F + G = Salsa and ChaCha = 52 (Intersection of Yellow Circle and Red Circle).
You are also given that:
G = Merengue + Salsa + ChaCha = 50 (Intersection of all 3 circles).
To find D, you need to subtract G to get D = 80 - 50 = 30
To find E, you need to subtract G to get E = 75 - 50 = 25
To find F, you need to subtract G to get F = 52 - 50 = 2
To find A, you need to subtract E, D, and G from BC to get:
A = BC - D - E - G = 129 - 30 - 25 - 50 = 24
To find B, you need to subtract D, F, and G from YC to get:
B = YC - D - F - G = 95 - 30 - 2 - 50 = 13
To find C, you need to subtract E, F, and G from RC to get:
C = RC - E - F - G = 89 - 25 - 2 - 50 = 12
You now have all the pieces.
You have:
BC = Merengue = 129
YC = Salsa = 95
RC = ChaCha = 89
The piece parts are:
A = Merengue DISABLED_event_only= 24
B = Salsa DISABLED_event_only= 13
C = ChaCha DISABLED_event_only= 12
D = Merengue and Salsa DISABLED_event_only= 30
E = Merengue and ChaCha DISABLED_event_only= 25
F = Salsa and ChaCha DISABLED_event_only= 2
G = Merengue and Salsa and ChaCha = 50
Your Total Number of dancers is equal to 163.
Add up all the piece parts and you get:
A + B + C + D + E + F + G = 156
The difference is 163 - 156 = 7.
Those are the dancers that do not know Merengue and do not know Salsa and do not know ChaCha.
Add those to the total of dancers and your total becomes 163 as given.
The Venn Diagram helps to visualize it, but you still have to know the logic of how to determine each of the piece parts.
|
|
|